|
||||
|
Before the game : board size, handicap setting, etc. The game in progress : legal moves Counting the final position : general principles Japanese troubles : what is a dead group ? Are White's complaints justified ? This document is written for any go player familiar
(well, reasonably fluent
Before the game : board size, handicap setting, etc. Go (or Weichi, if we are to mention its history) has at stake occupation and control of a grid, but this was probably not initially the object of the game, and actually the initial motivation of Weichi is clouded in mystery. It is well-known that the present grid (the 19×19 goban) is not the only one possible, and was for a long time coexistent with the 17×17 one, which may have appeared first, but, besides experimental games on 21×21, and beginner's games on smaller boards, it is only, oddly enough, games on 9×9 which may at times be seriously played by high-level players. It would appear logical if Weichi had always been played starting with an empty board, but this is not the case : in ancient China, games began with the four corner star points already occupied, and there existed even an old Korean variant where 17 stones were first placed on the board before play began (maybe under the influence of chesslike games, but the reasons are unclear) ; of course, these starting positions hindered the development of opening theory ...
The game in progress : legal moves If the game had really be created around the idea of control of a grid, the capture rule would probably have appeared as a consequence of the necessity of disposing of the invading opponent's stones. It is quite unlikely that this was the real order of events, and in fact modern rules are probably derived from an early primitive version (like the game of the first capture, aka atari-go), refined by the players' experiences (for instance, it becomes quickly clear that something must be done in case of
ko, if one wants the game to end at all |
||||
Counting the final position : general principles To understand the following analysis, one must keep in mind, as has already been said, that the
"historical" rules (as developed in China, and then in Japan) are only a codification of players' common sense (as a matter of fact, for a very long time, there were no written rules, and, in case of a dispute, one would simply consult the strongest player available). Even starting from the "first-capture game" it will soon appear to astute players that it is a good strategy to build large territories, where one will be able to play stones for a long time without the risk of being captured. . An important consequence is that a move in one's opponent's territory is now a bad move (if it is not, this shows the territory was not really his yet) ; this is true in Chinese and in Japanese versions, even if is is not so obvious in the Chinese one. In fact, it is even less obvious that playing in one's own territory is a bad move under Chinese rules. But a little thought will show that this is of even less value (if such a thing is possible Japanese troubles : what is a dead group ? Now the real problems appear: some decision process must be created to determine which stones are dead. Of course, such a procedure must not require either player to lose points
(otherwise, the previous difficulties will reappear) ; in rules where the proof of the death is done by actual play (this was for instance the case in my first writing of the (old) french rule, in 1972 ; one will find it in "Le
jeu à 9 pierres"), the position must be counted as it was before the dispute (this leaves various problems unsolved, of which I was blissfully unaware in those times As it happens, Japanese sensibilities (and maybe also their conception of the law) resulted in the treatment of this question neither by a practical procedure nor by a abstract general ruling, but in a case-by-case fashion. In fact, a rigorous definition of life and death is extremely difficult to formulate (see on this subject the rule "J89" and its revision (1997) formalized by Robert Jasiek). Moreover, all decisions already made becoming precedents, common sense arguments give no longer necessarily the results professionals have already agreed upon. Three examples will show how this is not at all a trivial matter. The most famous of those precedents is probably the one known as "Bent four in the corner" (Figure 1). Black has no move left. White can wait till the end of the game, then sacrifices 4 stones, plays back (at 1-2) to initiate a ko in his favour (i.e Black must find the first threat), and White wins the ko, since the game has ended and all the ko threats have disappeared.
Figure 1a : Same one, with a non-removable ko threat : by Japanese rules, White would win by
7 points ; in area counting , he may : a) not play, and lose by
9 points b) start the ko, not answer the threat, and lose by 8 points c) answer the threat, let Black recapture and win the ko (as White has no threats); White loses again by 9 points...(the reader should check those calculations ; he will note that in the initial position, Black and White played the same number of moves A careful analysis of the fight of figure 2 (left to the reader
.
On the other hand, both groups of figure 3 are capturable, but whoever captures first leaves the possibility of "under the stones" play. If Black begins, White scores 3 points (neglecting the ko, which could be a problem in itself) ; if White begins and then finds the tesuji of sacrificing three stones,White scores 2 points (and if he misses the tesuji, he scores only one point !). In short, each player would rather have the other one start the fight (as in a seki
The reader not yet completely disgusted will find on Robert Jasiek's home page a complete list of those strange positions (as far as one knows Chinese puzzles At this point, the reader should begin to agree that area counting displays some superiority in litigious positions. To be completely honest myself, I must admit that it suffers also from some imperfections. The main problem is that two "philosophical" visions are always possible : a "theoretical" one, saying that as soon as something is clear in the intuition of every player, like the fact that a white group without eyes and completely surrounded by a live black group is never able to subsist on the board, any rule must respect this knowledge (this is the Japanese point of view) and a "pragmatic" one (more "Chinese") saying (in its most radical expression) that if White can by any means prevent his capture, he has well earned his victory. Here is a spectacular example of what I mean : the "moonshine life". The NW corner group is not capturable, as White has an infinity of non-removable ko threats on the right. Almost every player feels that this is like cheating, and would rather ask the rule to prevent White from succeeding with this. In fact one discovers, when trying to play the sequence of threats, that the superko rule solves the problem : if White attempts to save his NW group, he loses everything (try it). But it is a close call In the same vein, some positions has been constructed (to the amazement of almost all strong players) where a normally live group (in seki) can be captured, as in the following situation …
White, with a clever use of the superko rule, can kill the black NW group ! It is not very hard, but the idea is quite hidden ; I will let you try to discover by yourself
the devilish trick of the White ko threat in the middle of the sequence, in spite of the absence of any ko, to force Black to pass twice and finally lose his group, because of the prohibited repetition. If you didn't find it, you are in good company Lastly, T. Mark Hall (BGA 4d), a few years ago (in a serious game), came across a perfectly plausible position (the "molasses ko") where the literal application of the superko rule leads to a completely absurd and monstrous conclusion. I recently discovered that with a slightly modified formulation of superko rules (due to Bill Spight), these difficulties disappear, but there is no guarantee that other troubles will not appear someday All this being said, the above positions are nevertheless exceptional, and they don't seem to give many serious arguments against area counting. So why does one encounter so much reluctance to count the Chinese way ? Ways of counting The real problem is that the majority of senior players were taught the Japanese way, and that the Chinese method is unfamiliar to them.
When discussing counting, it is important to distinguish between scoring (i.e. number of points in territories, value of prisoners, etc.) and the actual method of counting (with rearrangement of boundaries, placing the prisoners in opponent's territory, etc.) ; the Chinese procedure is much more spectacular, and ends by counting stones by lots of 10 So, one wants area scoring (if only to simplify the referee's task Are White's complaints justified ? At this point, one used to Japanese scoring can think that all of this is quite unfair for White, who will lose half of the games he would have won by territory counting (by half a point). In fact, nothing like that happens, but one needs a little bit more reflection (and calculation) to believe it. It may not be completely mandatory to open the window where the complete analysis of this question is done (if nothing appears, just click here), but this will, I hope, put algebraically minded readers at ease once and for all. Indeed, those calculations show that (under the previous hypothesis), White cannot lose "because of area counting". Of course, the reader will have already guessed that a few weaknesses subsist in this analysis First, area scoring allows getting points in seki. This is not so easy : here is the simplest case : a and b would be neutral points according to Japanese rules ; with area counting
White gets 2 points here. One can note again that Japanese rules are more "logical" (White has barely escaped here, so he got b only by the narrowest margin The other difference lies in the possibility of unilateral dames, i.e. playable by only one player. The opponent must then pass (and pay the usual penalty if one counts the Japanese way) while they are filled. A few examples of this are known (and they can get quite tricky to play optimally when one meets them for the first time) : it may, for instance, happen in connection with a "half point" ko in the last moves of yose, when one player has many more threats than the other : she can leave the ko open, then fill it, while her opponent can only pass (or play inside her own territory, which is no better). Actually, another "philosophical" question has not yet been discussed : what exactly is one supposed to prove by winning a Go game? It is always possible to argue that only the pleasure of having played good moves (or at least better moves than the opponent) is what matters. But if the point is to prove an expertise greater than the opponent's, it is clear that initial conditions must give equal chances to both. Yet the game is obviously biased towards Black (in the worst case, if Black's first stone would cause her to lose the game (very implausible), she needs only to pass to get at least a draw). 1) Every player makes publicly known (for instance at registration time in a tournament) a number (integer or half-integer) called his "favorite komi" (fk) 2) For every official even game (in a tournament where this system is applied, of course), the "real komi" (rk) is the mean of the "favorite komis" of both opponents. 3) The player with the larger "favorite komi" begins (and plays with black). In case of equality of fk, colors are drawn randomly… Commentaries : 1) Using this method, let's say that A declared a fk of 8 and B a fk of 4. This means they feel the game is fair with those respective komis. The procedure gives a real komi of 6, and A begins. A should be satisfied, as she must pay only 6 points to be Black while she thought this advantage should cost her 8 points ; B should be equally satisfied, as he gets a compensation of 6 points, and was prepared to receive only 4. 2) Some similar systems have been criticized for introducing a psychological dimension (a poker game) in the bidding period : let's say A knows that C hates playing with White, and is willing to declare 12 as fk to be sure to get Black. A has then only to propose 11.5 to get White and a komi of 11.75 points, while she could not hope for more than 8 if C knew A's fk in advance. This is the main reason for point 1) above : no such kind of manipulation is really possible, as every player must declare his fk before knowing who will be his opponents. 3) Of course, if rk is an integer, the problem of drawn games ("jigos") is back. But is this such a large inconvenience in practice ? |
||||
|
|
||||
|
|
||||
Solutions If a player doesn't wait for all the dame to be played before defending, he loses one point (or more White captures 4 stones (playing a1, say), Black cuts back at b2, White plays a2, sacrificing the 3 stones a2-a1-b1, Black captures them at a3, White plays atari at b3 and Black loses the a3 stone. White puts the NW group in atari playing a3, Black plays (and captures) at a1, White plays the ko threat at j6, Black answers j5 (let's call this the position *), White captures at a2, Black must pass, White plays a3 and Black is not allowed to capture (at a1), as this would return to the position * ! |
||||
|
|
||||
|
| ||||
|
Let's admit there are no more dames (they have just been filled in alternation, and there is no seki), and both players have just passed (for the first time). Dead stones have been taken off (and added to prisoners, if we are counting the Japanese way). The black territory (in the japanese sense, i.e the number of empty intersections) is b, the white territory is w, there are pb black prisoners (captured by White) and pw white prisoners. At this instant, there are therefore t=361-b-w stones on the board, x played by Black and y by White. If White played last, both players played the same number of moves, and so x+pb=y+pw, and x+y=t, so x=(t+pw-pb)/2 et y=(t+pb-pw)/2 ; those numbers being (of course) integers, this means that t+pw-pb is even. Or else, White passed first, and x+pn=y+pb+1, so x=(t+pw-pb+1)/2 et y=(t+pb-pw-1)/2. Japanese score (for Black) is j=b+pw-w-pb (minus komi). Chinese score is c= b+x-w-y (minus komi). One can check easily that this is exactly what the "rule of the first pass" takes into account, i.e. j=c if t+pw-pb is even, and j=c-1 if it is odd. Now, if White wins by one half point (in Japanese scoring, with a 5.5 points komi), it is because b-w+pw-pb= -5, so t+pw-pb=356-2b is even and there is no correction : White wins also by area counting. |
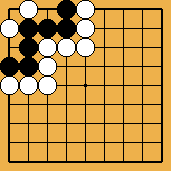 Figure
1 : « Bent four in the corner »
Figure
1 : « Bent four in the corner »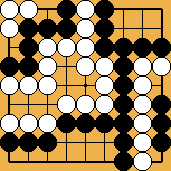
 Figure
2 : "Two dead, only one capturable"
Figure
2 : "Two dead, only one capturable"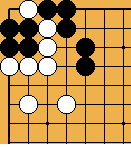 Figure3 :
« 3 points without playing »
Figure3 :
« 3 points without playing »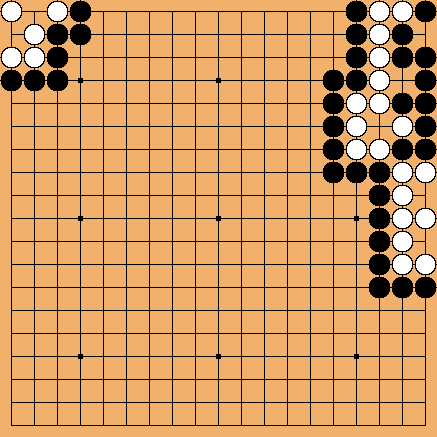

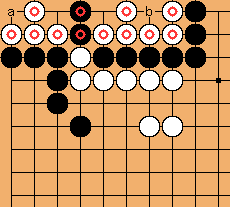
 For instance, in the opposite figure, White can play at any time moves 2 and 4 without destroying the seki, but Black cannot play at all, as if she plays 2, for instance, White answers at 4 and the black group dies ("bulky five"). Area scoring adds therefore 2 points to White territory, and counting the Japanese way (aka "fast counting method") gives the same result (if White plays correctly, i.e. after all external dames are filled) by making Black pay one or two pass stones (depending on who filled the last external dame). It is for those situations that the following clarifications (not completely explained in the
For instance, in the opposite figure, White can play at any time moves 2 and 4 without destroying the seki, but Black cannot play at all, as if she plays 2, for instance, White answers at 4 and the black group dies ("bulky five"). Area scoring adds therefore 2 points to White territory, and counting the Japanese way (aka "fast counting method") gives the same result (if White plays correctly, i.e. after all external dames are filled) by making Black pay one or two pass stones (depending on who filled the last external dame). It is for those situations that the following clarifications (not completely explained in the