|
Introduction
I. Extraordinary life and death problems.
II. Paradoxical tesujis and strange manoeuvres.
III. Ladders and other incredible sequences.
IV. Semeais, sekis and pseudo-sekis.
V. Problems about rules.
Appendix A: some (badly connected) thoughts upon the "theory" of go problems.
Appendix B: a few tries at (almost) rigourous definitions.
Back to Part 1
Back to¨Part 2
III. Ladders and other incredible sequences.
Most of the sequences of this section are, one must admit, very artificial. But this doesn't make them less pretty (or less funny), and, as Cyrano de Bergerac says (in the Rostand's play) : "No, no, it is even more beautiful when it is useless..."
"If you don't understand ladders, don't play go", says the proverb. Well, they do not look so hard to understand, even if they relate to many subtle theoretical questions, such as the cost of pushing a broken ladder (as ko threats, say), which is estimated (to the astonishment of many players) to be 7 points for each extra stone. But in spite of Kageyama's warnings in the first chapter of "Lessons in the Fundamentals", every 10k player thinks he is able to read a ladder. Nevertheless...
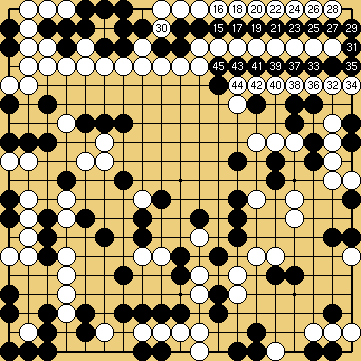
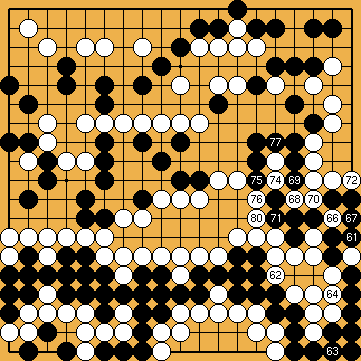
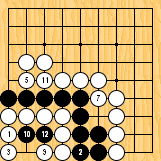
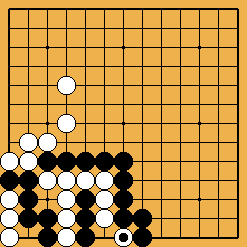
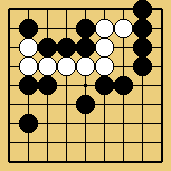
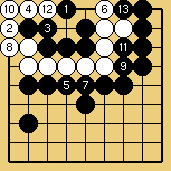
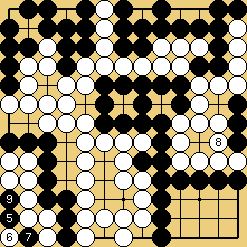
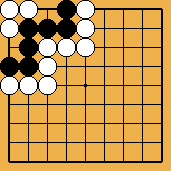
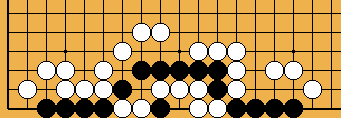
The invasion of problem 1 (it is detailed in this sgf file) is often played, against many handicap stones, by white players who don't suspect the extent of the punishment they could receive if Black really "understood" ladders. The old-fashioned joseki of problem 2 was carefully studied in Ishida's dictionary (I tried to show a few variations in this sgf file) ; in the good old times when it was still played in tournaments, the traps which appear (especially the ladder shown here) gave often to French players many pleasant results. Last (problem 3), the disaster which befall O Meien in 2000 while playing the first game of the 55th Honinbo tournament (here is the sgf file of the game) is clear proof that modern professionals are no longer ashamed of there (exceptional) off-days : after such a mishap, I believe a mortified Shusaku would have spent a few months meditating in a monastery, but O Meien just resigned the game (laughing out loud), then went on winning the next ones, and the title.
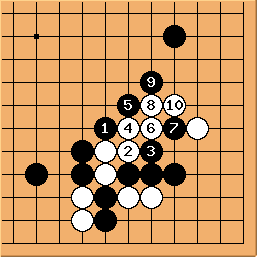
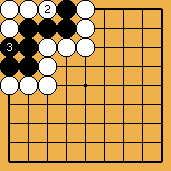
Solution 1 : the white stone is not a ladder break
Solution 1 (next) : it is a kind of squeeze
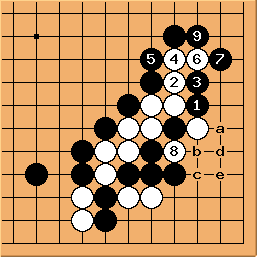
| | 
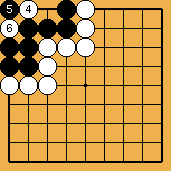
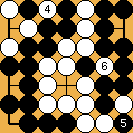
Solution 2 : here, the ladder starts on the first line
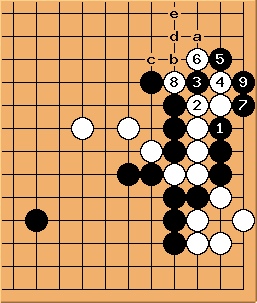
| | 
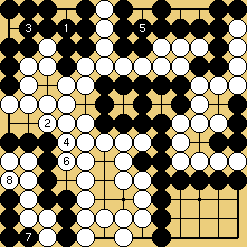
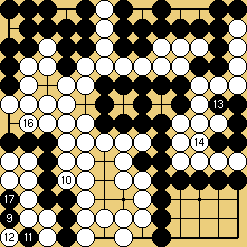
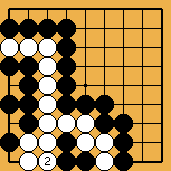
Solution 3 : the white wall is swallowed (O Meien didn't push for so long...)
|
On the other hand, you need not be ashamed of yourself if you fail to solve the following problems without trying sequences on the board...
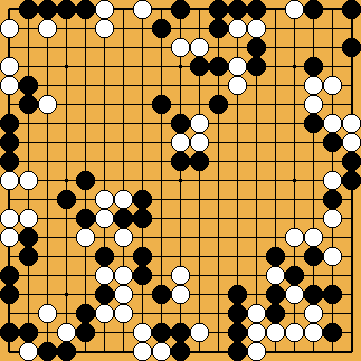
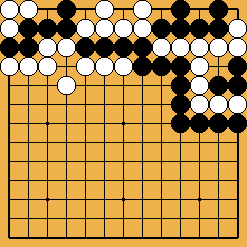
   Problem 4 : White to play and save the SE corner group Problem 4 : White to play and save the SE corner group
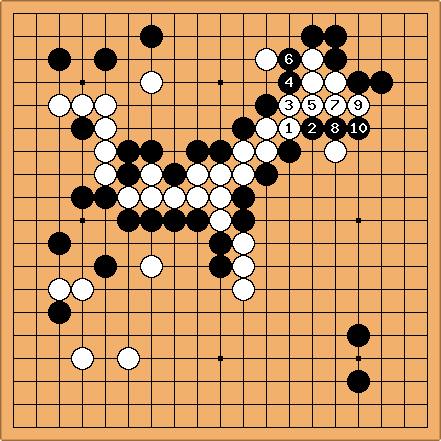
Some professionals specialize in composition of spiral ladders crisscrossing the board ; problem 1 is a rather nice example, requiring some care in the beginning. These highly artificial labyrinths may look completely useless, but solving them with the eyes only is, at least, a tremendous exercise for one's eye muscles...
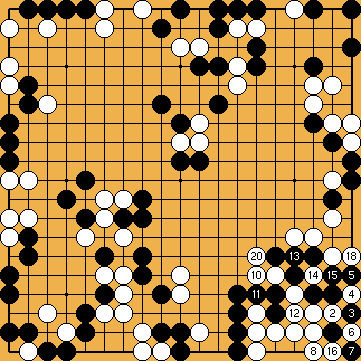
Solution 4 : I only show the ladder start ;
click here to see the whole sequence
Many other wondrous sequences of this type have been created, Nakayama Noriyuki being an expert at figurative settings such as hearts, kanjis or year numbers... But I also found a few "engineered ladder problems", which are "only" improvements on known themes ; the most astonishing is probably the following :
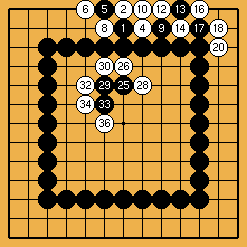
This Genran problem (the Akubotsu Intetsu collection mentioned here) is an improvement on Dosaku's sacrifice (problem I.4.12) : the under-the-stone play (here turned towards the center) ends in a very windy spiral ladder.
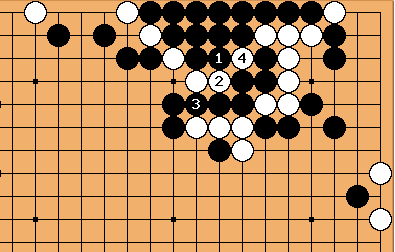
Solution 5 : a 14 stones sacrifice
| | 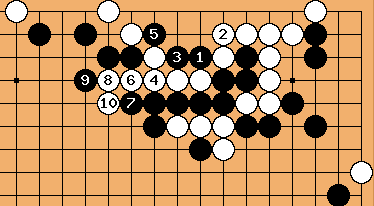
Solution 5 (next) : first steps in the ladder
| | 
Solution 5 (conclusion) : did you read it to the end ?
|
Now, for something completely different...
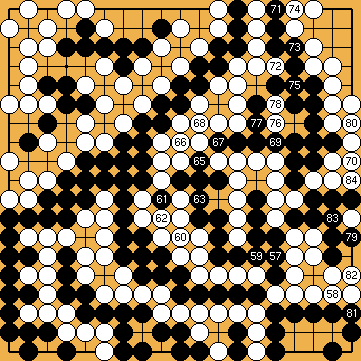
Problems 6 and 7 (classical problems from Xuan Xuan Qi Jing, whose refinements shown here were given to me by Pierre Colmez, and which one could almost believe come from real games) are ladder construction problems : in both cases, one or two groups can live if a specific ladder is not broken ; you must first find the ladder(s) (a quite tricky operation in the case of the NE group in the second problem, as Pierre and I discovered, during the summer of 2007 : a mistake had found its way into the solution diagram, which nobody had noticed... for the last twenty years) then play a move which "unbreaks" it (or them).
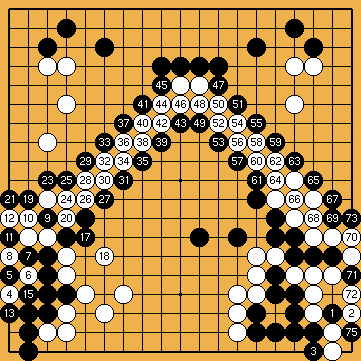
Solution 6 (14 at 11, 16 at 5, 22 at 9, 74 at 71) : to unbreak the ladder, one must play
in the most unlikely place ; one will then be treated to the pretty finish in double snapback
Click here for an animated solution
|
|
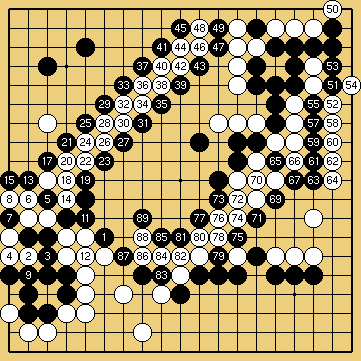
Solution 7 (10 at 7, 16 at 5, 56 above 55, 68 at 65) : here, two ladders must be unbroken ; the second ladder, as a bonus, is not really easy to start ...
Click here for an animated solution
|
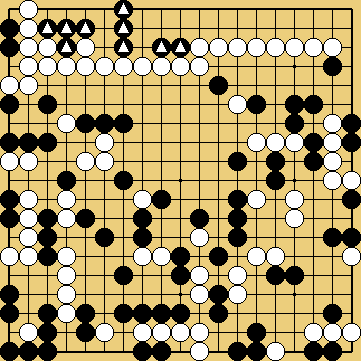
   (?) Problem 8 : White to play and capture the marked stones (?) Problem 8 : White to play and capture the marked stones
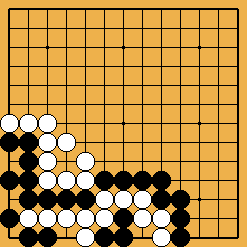
Problem 8 (which I found in Nakayama's book, but it was created by Hayashi Genbi, in early 19th century) is an incredible loose ladder ("path of two liberties" or yurumi shicho) crossing the whole board.
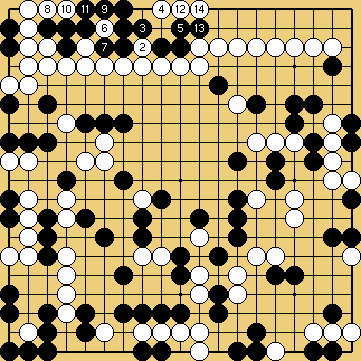
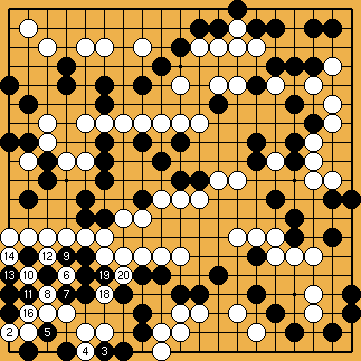
Solution 8a : starting point. Now, White find a surprising first line attack...
| 
Solution 8b : ... which leads to a loose ladder | 
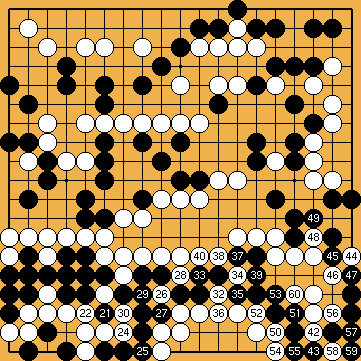
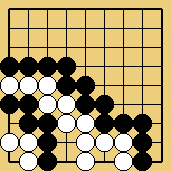
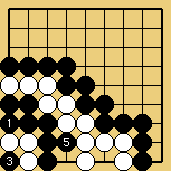
Solution 8c : conclusion. This is truly an astonishing composition ; to calculate this sequence (without putting stones on the board) really is quite hard, even for pros. If you didn't succeed,
click here for an animated solution
|
    Problem 9 : White to play and save the marked stones Problem 9 : White to play and save the marked stones
Problem 9 (from Hatsuyoron) is also (in some sense) a loose ladder, but I prefer to see it as an exercise in construction of dangos ("dumpling" : those amorphous and inefficient groups of stones French players call "pâtés", not as a reference to food, but to the "pat-a-cakes" of sand moulded by children on the beach). Quite often, as here, the Hatsuyoron problems are also tasks, i.e. they attempt to get the maximum effect of some theme : here, some of the dangos appearing along the way (for instance the 3x5 solid block in the center) are record-breakers, especially after looking at the initial reasonably light shapes. It is, however, almost impossible to show the complete solution with diagrams, so I give below an animated version...
Solution 9a : the starting point : big eye construction
(White has 9 liberties)
| | 
Solution 9b : the squeeze spills towards the corner
| 
Solution 9c : first dango in the centre. Now what ?
|
|

Solution 9d : conclusion : one must be quite strong
to find his way out of this maze.
If you didn't succeed,
click here for an animated solution
|
To close this section, here are
the most astonishing seki construction sequences I have ever met (the one in Hatsuyoron, which will surely appear someday on these pages, is not to be scorned, but I feel it is slightly less interesting, if more correct, as the fights appearing in it are not so involved)

   (?) Problem 10 (No Man's Land) : White to play; what happens if he tries to save the south side group ? (?) Problem 10 (No Man's Land) : White to play; what happens if he tries to save the south side group ?
I met problem 10 (No Man's Land)
on this very diverse site of problems for all levels. The caption lacks perhaps of rigor ("White to play and win the game" would be better...), and some mistakes could have entered this composition, but the fact that the author is a kyu player compensates for these possible weaknesses...

Solution 10a : seki for the moment. Now, Black attacks the outside groups
| 
Solution 10b : there is still one playable semeai left
| 
The end. It seems (but I didn't check) that this variation is a half point win for White...
Click here to see an animated solution.
|

    Problem 11 : White to play ; what is the result ? Problem 11 : White to play ; what is the result ?
(click here for an sgf file of the solution)
Problem 11 is the penultimate problem in Genran, and must be the best classical problem of seki construction. Here again, the caption is not clear (is White forced to start in the NW corner ?), and some mistakes might still blemish this masterpiece (for instance, I do not understanfd the order of moves in the center, nor the status of the SE corner); one will find more thoughts on this matter in the annex... A solution (not yet commented) appear in the associated sgf file.
Solution 11a : the 10 first moves
| 
Solution 11b : the end (if White doesn't play 2, he loses the fight in the center by one liberty)
|
Back to the table of contents
IV. Semeais, sekis and pseudo-sekis
The problems and positions of this section (and the following one) are clearly less interesting and beautiful that those shown before. But this is one of my pet subjects (I actually did compose some of them), and I could not resist the opportunity to present here some results that would surprise even professionnals (but probably would not really interest them much  ) ... ) ...
A semeai ("race to capture") is a fight between 2 or more groups, both or all unable to live, which can only end by the capture of one of these groups, or by a stalemate equilibrium (a seki). Those definitions are not really satisfying for a mathematical mind, and I refer to the Appendix of this bestiary (once it is complete) for something somewhat more satisfying (Japanese rules connoisseurs know that to define completely rigorously the notion of seki is an almost impossible task, even if it is quite possible to get a reasonably practical definition)
1. Simple semeais and count of liberties
In fight between two groups, the one with more liberties wins the race... This "proverb for two-digits kyu players", already neglecting the possibility of seki, suffers meny exceptions, as we will see below.
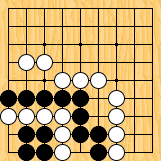
As a starter, let us recall the first really interesting case of semeai. Can you guess who wins the fight in figure 1 ?

 Figure
1 ("the house") : « is Black really ahead by 10 liberties? » Figure
1 ("the house") : « is Black really ahead by 10 liberties? »
An useful proverb here is "3-5-8-12-17" (though, for a proverb, it does lack literary qualities), giving in turn the actual number of liberties of big eyes. Here, for instance, White has a 7-space eye, where two stones have already been played, meaning he has 17-2=15 effective liberties, which implies that the side beginning the race will win it (by one move) ; if you dont find this fact obvious, try to convince yourself by putting the stones on a board, or with the help of this
animated solution.
 Figure
2 : in this case, White cannot really be confident of having 9 liberties... Figure
2 : in this case, White cannot really be confident of having 9 liberties...
These formulas will be useful in some of the following analysis ; one must nevertheless aknowledge they admit of a few exceptions, as some "big eyes" in the corner, like the one in figure 2, have to concede many of their liberties to prevent the formation of what James Davies calls "an eye in the belly" ; the observant reader will notice that this explains the possibility of the strange seki in problem V.12, and of the one in figure 3bis...
Solution 2 (4 at 10, 6 at 12, 8 right of 3) : actually, Black wins the race by one move
One of the consequences of the preceding formula is that it should be impossible to get a seki in semeais between groups with different-sized eyes, because the player with the bigger eye starts by filling all mutual liberties except one, then captures the inner stones (if any), getting back enough liberties to be able to fill the last mutual one and win the race. This is a well-known argument (with a corresponding Japanese proverb "o me, ko me", i.e. "big eye / small eye") and obviously irrefutable... except that, to our astonishment, it was refuted by Paul Drouot (in a game commentary, when he was only 2-dan), with the following position :
 Figure
3 : does White's big eye break the seki ? Figure
3 : does White's big eye break the seki ?
Don't worry : the other better-known proverb ("me ari, me nashi" = "one eye against no eye" = "in the land of the blind, one-eyed men are kings") looks secure (but will you still be confident of that at the end of this section ? The astonishing circular hanezeki of figure 13 could make you doubt). I thought figure 3 was a French secret, but I was surprised to discover it in the semeai book (Counting Liberties and Winning Capturing Races) published by the British Go Association.
Figure
4 : a strange seki, courtesy of computer play...
Even if it is not exactly another refutation of the proverb, the semeai in figure 4, which could only appear in computer play (or with very weak players), and which I discovered in March 2008 while watching one of the "MonteCarlo" programs (the best-known of those being MoGo), is another instance of the same curious phenomena (i.e. that the owner of the large eye must reduce it in order to start the fight, losing his liberty advantage). This fight ends in seki, and its not even a complete one : by correct play, Black may (after the last significant moves have been made) win 9 points (in area rules ; Japanese would only count 6), while White is defenseless (of course, as soon as only 2 mutual liberties are left, Black must start the fight by capturing the 3 stones, and White must then pass, and not fill the tempting mutual liberties...)
Solution 4 (2 passes, 4 at 2-2, 6 at 2-1, 7 above 3, 8 at 6) :If Black begins, she scores 9 points (the 6 prisonners, the destruction of the two eyes of the other seki, and the stone played at 1)
Except for the previous positions (and a simpler variant which we'll meet in the rules section), the only other unusual thing that can happen (to our present knowledge) in fights without ko between two groups is the hanezeki (and not 'hane seki', this common misspelling was pointed out to Harry Fearnley and myself by John Fairbairn) of figure 5 below ; this strange position, in which the marked stone cannot be captured without destroying the seki, is the main theme of Dosetsu's problem, where the stones in atari, but which are not actually capturable, create havoc in White position. One will note that it is, again, a consequence of the difference in liberty count between two eyes of different sizes, as capturing the external stone enlarges the opponent's eye when he recaptures ...
 Figure
5 : hanezeki ; the marked stone cannot be captured. Figure
5 : hanezeki ; the marked stone cannot be captured.
Of course, semeais appearing in real games are not always as easy to count, as external liberties are not often already filled when the race starts. Moreover, some of those liberties may become hard to fill, as in the nice following problem:
 Problem
6 : Black to play and win the race Problem
6 : Black to play and win the race
The corner group is dead (this is left as an exercise to the reader...), but, by threatening to live, and while having only 3 apparent liberties, it will win the race...
Solution 6 : actually, Black is one step ahead, as 3 approach moves are needed to fill the liberties...
When kos are involved, the semeai theory has been less studied (although there is often truth in the rule saying that one must capture the ko only at the end), but one must still look hard to find, if not truly paradoxical, at least really strange situations ; I discovered (during the spring tournaments of 2007) that fights with a "bent four" may depend of the exact structure of the external ko threats. In the almost identical semeais below, Black can win the game, but she must not play them in the same way ...
Solution 7 : Black can remove
one White ko threat, then...
|
|
... force White to play a
disadvantageous ko
|
Solution 8 : in this case, Black can
remove 3 ko threats... |
|
and still have time to play the
other ko (advantageous to White), because
of her permanent threat (15 at 11)
|
2. Semeais between three groups
Fights between three groups can already become quite complicated. The seki in figure 1 is well known, even if many "older" players are surprised to learn that it is counted as two points for White in area rules like the AGA's, but similar positions (with bigger eyes) have strange behaviours : first, figure 2 ("both dead, only one capturable") is what I call a half-seki : White has no play left, as if he adds one move, he loses both groups ; Black may, whenever she wants (after the filling of dames, therefore) capture any group, but the other will then live (check it). If there are mutual liberties left, the situation is stranger yet : in figure 3, White has again no play left, but when Black fills a liberty, White must follow suit, to get at last a position similar to figure 2 (else, he loses both groups). By the way, these positions could also appear in the rules section, as it is hard to argue against the fact that both White groups are dead, a status which is not, for Japanese-style rules, easy to manage and still get a sensible score of the position...

  Figure 4 : a complete seki Figure 4 : a complete seki
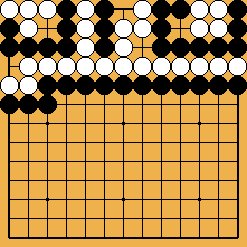
   Figure 5 : what is the difference ? Figure 5 : what is the difference ?
| |
Figure 4 displays a new type of complete seki (i.e. a position where adding even one move breaks the seki) : the stones in atari cannot be actually captured, as the semeai is then lost by the taker. Curiouser and curiouser, the position of figure 5 (found by André Moussa and myself in 1985), which appears similar, is in fact another kind of half-seki : White cannot do anything, but when Black captures the square block, and next the other 4 stones, White has no time to kill the second group, and must compromise to a new seki, while Black has scored 11 or 12 points, depending on the rules (by the way, if Black erroneously starts the fight by taking the T-group of 4 stones, she loses all her groups ; this quite counterintuitive behaviour is the reason I gave 3  's to the position). To conclude, there is no possible seki between 3 groups with even larger eyes : the player with the bigger eye is enough liberties ahead to win the race ... except in a completely artificial case, discovered by Harry Fearnley in Summer 2005, and shown below (figure 7): in this position (as in figure 2), White's big eyes are smaller than they look... 's to the position). To conclude, there is no possible seki between 3 groups with even larger eyes : the player with the bigger eye is enough liberties ahead to win the race ... except in a completely artificial case, discovered by Harry Fearnley in Summer 2005, and shown below (figure 7): in this position (as in figure 2), White's big eyes are smaller than they look...
UPDATE ! (summer of 2010) I thought I understood completely the behaviour of those fights when, in 2010, I discovered figure 6, which is another complete seki, but in a quite surprising way : if Black add a move, she loses all her groups, but if White plays, Black reverts the position to figure 5, then scores 11 or 12 points...
|
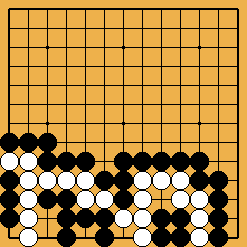
 Figure 8 : an asymmetrical seki Figure 8 : an asymmetrical seki
| |
I discovered in August 2004 the strange complete seki of figure 8, a refutation of one of my conjectures (I thought that the two white groups had to be of the same eye size). Are there other similar oddities yet to be discovered ? Is something even stranger than the hanezeki still lurking somewhere ? |
3. Four groups and more


  Figure 1 : 3 complete sekis Figure 1 : 3 complete sekis
| Beyond that, as fights with four or more groups have low probability of appearing in actual games, the following examples (some of them byproducts of the mathematical theory developed by Vladimir Gurvich) would look artificial and uninteresting if they didn't allow new counterintuitive phenomena to appear : first, the three wheels of figure 1 are complete sekis ; this looks absurd, as one goes from one to the next by filling liberties, but I let you check that instead of following suit, the second player can then in each case win the semeai (as a completely off-topic aside, I discovered also that they give rise to a strange optical illusion ; I can assure you that these positions are perfectly square, in spite of what your eyes tell you)

|
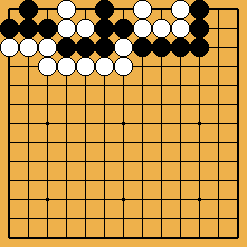
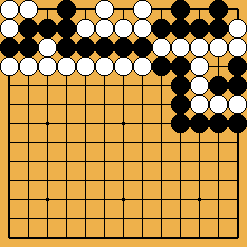
  Figure 2 : mock sekis (sacrifices are playable in two of those positions) Figure 2 : mock sekis (sacrifices are playable in two of those positions)
|
The three tangled positions of figure 2 look like complete sekis ; but it is in fact true only for the first one, as a new possibility appears : both players may sacrifice one of their groups to capture another ! This is why the third position is a win for Black (by sacrificing the corner group), and the second one is a complete seki, but only because if one player tries to break it, he loses two points...
|
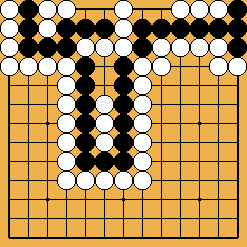
  Figure 4 : another example of half-seki Figure 4 : another example of half-seki
| |
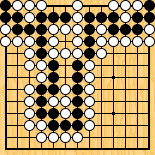
  Figure 5 : a difficult semeai Figure 5 : a difficult semeai
| |
But figure 4 (which I found too in 2004), is not a seki : as in figure 2.2, Black has no move left (else she loses the 3 groups) ; White can capture the largest group, but then Black will save the next largest, and White will not even need to capture the third, already dead group... In 2010, I realized that figure 5 (which is similar, but with larger eyes) had an even more complex status : if Black starts, she can only save her smallest group, while White, by starting the fight, captures again two groups, but must let Black save the intermediate one : this is a case of what I call a pseudo-seki. |
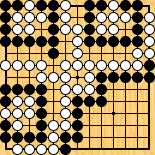
  Figure 6 : a mock seki, too good to be true ... Figure 6 : a mock seki, too good to be true ... | |
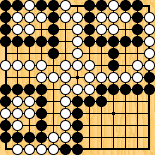
  Figure 7 : another hard semeai Figure 7 : another hard semeai | |
In the summer of 2010, having another look at the computations used in the construction of figure 3, I believed for a short time that I had discovered many new complete sekis with a large number of mutual liberties, the one of figure 6 being probably the most spectacular. It is not very hard to understand why I thought it should be complete : if White starts the race against one of the three groups, he must fill the mutual liberties, so the attacked black group has 11+7=18 effective liberties, while the white one has only 1+2x(7+1)=17, and loses the race by one. But if Black attacks, she must start by losing one of her own liberties, White counter-attack then by filling another liberty of the same group and wins the race (the count being now 16 against 17). The reader will already have guessed that some bad mistake crept into the previous analysis ; which one, and why isn't figure 3 similarly flawed ? Nevertheless, it is possible to construct, on the same scheme, semeais with strange behaviour : in figure 7, if Black starts, she captures the white group, but if White starts, he gets a result similar to figure 4, capturing two of the black groups, but letting Black save the intermediate sized one.
|
In conclusion, some exemples with 5 and 6 groups : figure 8 is similar to the previous one, but with a twist
(White has no move left, and Black may capture the central group and any one of the others, but not both) ; Black must start at a to capture the largest group, a fact which is all but obvious... Figure 9 is a semeai in which both players, to win something, must sacrifice one of their groups (I leave the diligent reader to find which one, and why) ; in all similar examples, the optimal sequence is quite hard to find, and a player may easily lose all his groups if he is not skilful enough...
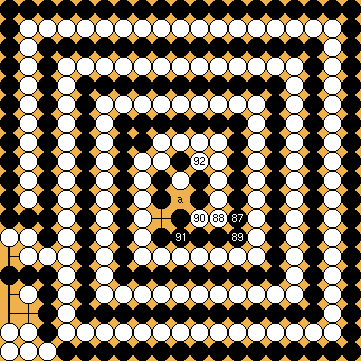
Figures 10 and 11 (but not 12) are complete sekis with 3 mutual liberties between some groups ; it was not known before 2011 if it was possible to top that, given, of course, that the example with 4 liberties of the Korean "blind spot" problem doesn't count. Figure 10 (well, a structurally equivalent one, but with a lot more stones ; the idea behind the simpler position shown here is mine) was constructed by V. Gurvich in 1981 (the main objective was to exhibit a defect in the Ing rules, which were at that time counting fractions of points in sekis, and were giving a list of examples of all the possible cases...) ; I was able to improve on this again in 2007, getting figure 11, where sacrifices are completely impossible. As for diagram 12 (which I find quite elegant), I also constructed it in 2007, using Gurvich's more recent results ; it would be an unbelievable complete seki with every group having 6 mutual liberties, except that one almost needs a computer to check that indeed any player adding one move must then enter a sacrifice sequence (else he loses everything), but one after which, as strange as it may appear, the score is not changed, even under Chinese rules. The mathematically inclined reader (it is hard to believe any other kind of reader would still be here...) will of course understand that is is not possible to eliminate these sacrifice variations just by putting all the relevant groups in contact, as it is well-known that the graph K3,3 cannot be imbedded in the plane ; this is why I am quite proud of figure 11...
UPDATE ! (summer of 2012) In 2011, studying again some variations of Dosetsu's problem, Harry Fearnley discovered a new type of seki, which he called circular hanezeki (figure 13), with at least 6 interlocked groups (not to mention a "one eye vs no eye" fight, nevertheless ending in stalemate), solving at last the Gurvich question. The diagram I show is a complete seki, in spite of the 5 mutual liberties (if White had only 4 liberties, Black could capture the 3 stones, destroying the hanezeki, but winning the race ; if Black had only 4, White could capture the chain, sacrifying his corner group, but winning the race against the one-eyed group) ; the diligent reader should find easy to construct similar complete sekis with many more liberties (14 seems to be the maximum), just by enlarging the nakade sizes.
Back to the table of contents
V. Rules problems.
This last section looks at a few positions which have given trouble to players and referees since the game was taken seriously enough to induce a codification of the rules. Most of them are studied, from a different point of view, on my page of thoughts upon the rules ; you will find below (among other surprises) positions hard to count the Japanese way (figures 1, 2, 3 and 4), and positions with a counterintuitive status under Chinese rulings (figures 5 and 10), not to mention the (in)famous molasses ko...
|
 Reference figure 1 : "bent four (in the corner)" Reference figure 1 : "bent four (in the corner)" |
How to capture (the "bent four" is the chain of stones sacrificed) ... |
How to capture (continued) : |
|
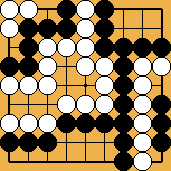
 Figure 2 : same bent four, with an unremovable ko threat Figure 2 : same bent four, with an unremovable ko threat
|
The best-known (and only one often found in real games) of those problematic positions is "Bent four in the corner" (in Japanese, magari shimoku), the traditional name given to the reference situation of figure 1.
The standard proof of capture, explained in the following figures (showing that this is another kind of half-seki, by the way) collapses if Black has (as in figure 2) unremovable ko threats. The Japanese rules (in the new 1989 version) still judge the black group dead, and give analysis tools proving that the black group is also dead in figure 3 (which would depend on possible irremovable ko threats with Chinese rules). On my page about rules, I analysed more precisely the various White options in the position of figure 2 with area counting ; the diligent reader will check that while White wins by 7 points, Japanese counting, his best line of play (not so easy to find) still lets him lose by 8 points under AGA rules...
|
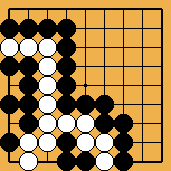
 Figure 3 : a "generalized" Figure 3 : a "generalized"
bent four |
|
The capture sequence ... |
|

The capture sequence (continued) : Black has no ko threats, as the game is finished |
Japanese players had good reasons for wishing to adjuge these exceptional positions (all half-sekis, it will be noted) without having to play them (which would usually be unfavorable for the first player) ; this is also the motivation behind the special rule for figure 4 ("torazu sanmoku = three points without playing" ; I call that one a pseudo-seki); I give a detailed analysis for AGA counting (in French, alas, but a translation by the BGA is now available on GoGoD's New in Go site) on my page about the French rules ; you may also find of interest the thoughts mentioned above (in English).

 Reference figure : 2 and 4 are one-sided dames Reference figure : 2 and 4 are one-sided dames | |
AGA rules (following Chinese ones, which, by the way, have quite recently been discovered to be actually posterior to the Japanese rules) use area counting, which prevents all this chicanery, as it only considers stones effectively played. It will be found, for instance on my page about rules, a proof of the fact that the winner (and even often the score) is usually the same with both rules, but exceptions exists, besides the counting of points in sekis, because of possible one-sided dames, i.e. dames playable by only one player. The opponent must then pass (and pay the usual penalty if one counts the Japanese way) while they are filled.
A few examples of this are known (and they can get quite tricky to play optimally when one meets them for the first time) : it may, for instance, happen in connection with a "half point" ko in the last moves of yose, when one player has many more threats than the other : she can leave the ko open, then fill it, while her opponent can only pass (or play inside her own territory, which is no better).
One-sided dames appear also in some "shape sekis". For instance, in the opposite figure, White can play at any time moves 2 and 4 without destroying the seki, but Black cannot play at all, as if she plays 2, for instance, White answers at 4 and the black group dies ("bulky five"). Area scoring adds therefore 2 points to White territory, and counting the Japanese way (aka "fast counting method") gives the same result (if White plays correctly, i.e. after all external dames are filled) by making Black pay one or two pass stones (depending on who filled the last external dame).
|
  Figure 5 : "moonshine life" ; Figure 5 : "moonshine life" ;
are the 4 white stones in the corner really dead ?
|
|
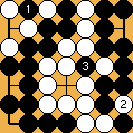 Figure 5 (follow-up) : anyway, they cannot be captured ! (4 takes back 1) |
A rule saying that the four white stones in the NW corner of figure 5 are alive would be felt completely unfair by anybody (except perhaps absolute beginners). Nevertheless, they cannot be captured : the configuration on the right is what I call an active seki, and White disposes there of an infinity of irremovable ko threats (as does Black, by the way), as will be seen in the follow-up figure. This scandalous situation was historically solved in two completely different ways : the Japanese rule adopted the "intuitive" solution, but with quite fuzzy means, using a not completely clear notion of independent life ; actually, in the 13th century, there really was a precedent, and White was, against all expectations, allowed to keep his stones on the board (this is Nyobutsu's Judgment) ; the complicated story of this ruling was eventually ended by a decision favoring Black, but only in 1949 ; as for the AGA (and similar) rules, they expose the fallacious reasoning of White's defence, capturing all its stones, if he insists, by a strict application of the superko rule, as shown below
 Solution : under AGA rules, 6 is not allowed, as it would reproduce the starting position of figure 5 ; therefore, this sequence would entail the loss by White of all his groups. |
|
The superko rule, or some variant of it, like the Japanese rule which says that any repetition other than a ko results in the voiding (mushobu) of the game (it must be replayed) is necessary, as some classical positions (other than ko) forcing repetition do exist : the main possibilities are given below (proofs of the forced character of the sequences are left to the diligent reader  ) ; "round robin ko" seems an artificial creation, but instances of the other three cases shown have already appeared in professional games. ) ; "round robin ko" seems an artificial creation, but instances of the other three cases shown have already appeared in professional games.
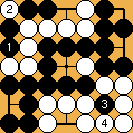
   Figure 10 : is the NW white group really alive in seki ? Figure 10 : is the NW white group really alive in seki ?
The simplicity of the superko rule compared with the Japanese version must not mask the considerable practical difficulties it would involve for players and referees in real games, nor the existence of a few perverse side effects : in the position of figure 10, the white group in the NW corner (a position known as "bent five") seems clearly alive in seki ... nevertheless it can be captured in this case by a strict application of AGA (or similar) rules, as shown below. The problem could obviously be ruled out by stipulating, for instance, that the superko rule applies only when no player has passed in between (this follows a recent proposal by Bill Spight, which would also solve some of the problems created by molasses ko), but it goes without saying that such ad hoc rulings always leave open the possibility of new freakish discoveries (and in fact Bill Spight had to word it more carefully to take care of the "sending two, returning one" position). Moreover, many players feel that any Black player able to find the difficult sequence of capture has fully earned her victory ...
 Solution : the strange ko threat 3 (played while there is no ko on the board)... |
|
 ... forces White to pass at move 6, then prevents him to capture 5 and 7, as this would reproduce the position on the left ! |
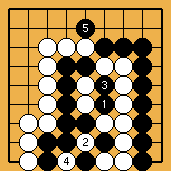
The semeai in figure 11 is probably the worst known case of repetition. Known as "molasses ko", this position arose in a real (but friendly) game played by T. Mark Hall, a British 4 dan ; a careful analysis of the fight (which can be found in the attached sgf file, or here) shows that the capture sequence below is continually forced (as long as no large ko threats appear), but nevertheless, the game may continue on the outside at 20% of its usual speed. Then, after the filling of the last dames, the player losing on the board may force a repetition (and so void the game) with Japanese rules, but with AGA rules (or with any "simple" superko rules), the players enter something extremely counter-intuitive (and very hard to play well) : a "pass fight", as it is easy to see that the first player to pass will next be unable to complete the cycle because of the superko prohibition (this, at least, could be prevented by adoption of Bill Spight's proposal...)
 Solution : the sequence is forced until 5 ... |
|
 ... which White can answer ar last at move 10 |
Other even less frequent (not to say completely impossible in a real game) examples of positions challenging some rulesets will be found on the websites of Harry Fearnley, and Robert Jasiek.
To be complete, here are finally some go analogs of fairy chess problems : a few of the strange new possibilities appearing with more radical changes to the rules, or to the objectives of the problems.
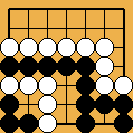  Position 12 : self-captures allowed ; what does this change ? Position 12 : self-captures allowed ; what does this change ?
The above position (due to a Dutch composer, Ger Hungerink) is the simplest example of a self-capture (allowed by the New-Zealand and Ing rules) changing the status of a fight (in the usual examples shown, it only creates new ko threats, which is clearly less fun) : with the usual rules, this is a "big eye beats little eye" semeai, one therefore lost by Black ; but after Black's self-capture, notwithstanding the fact that it is White's move, he can now get no more than a seki ...
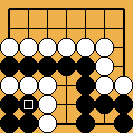 Solution : after Black self-captures her four stones... |
|
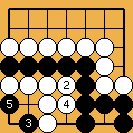 ... White cannot get more than a seki |
Now, for something completely different, three problems with quite unusual captions
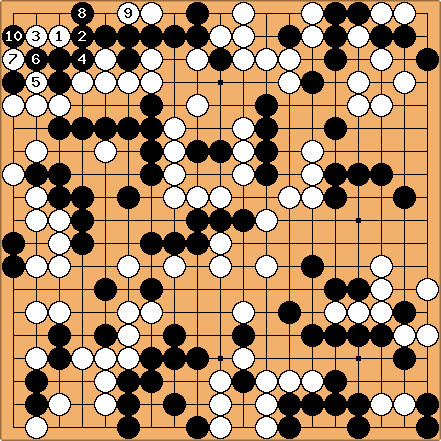
In the first problem, it is understood (as in any problem of retrograde analysis) that the move sought has only to satisfy the question asked (which means one is allowed to choose the position before the black move to be retracted, as long as it was a legal one). You should then be able to come to the only possible solution :
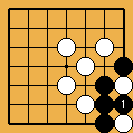 Solution 13 : this was the previous black move |
|
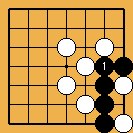 What Black should have done |
|
The second problem is my own "improvement" (found in Grenoble, in 1987) of another Ger Hungerink's creation (shown below as a variant). This kind of problem is usually understood as asking both players to play the best moves after the first initial "mistake' (it is not, therefore, an "help mate" problem) but here, the situation is much stranger, the black group starting alive and being left dead after the key, even if White then passes...
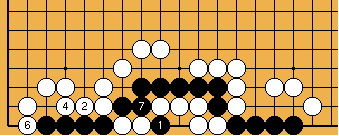 Solution 14 (8 two spaces left of 1) : after move 1, Black can no longer save her group, even if White passes ! |
|
 Variant : After the key move of solution 2, if suicide is allowed, Black can still live : it is possible to self-capture this stone, reverting to the initial position, where Black was alive (with a "2 and 3")... |
The last problem should be easier, but the result is quite unexpected : Black is dead ! The sequences shown below should be proof enough that Black cannot play (without getting captured) farther than the second and fourth line ; so her wall is captured without much trouble ... A really unfair rule, that one
 Solution : black stones disappear soon after having been played ... |
|
And to conclude with a last gem, what follows is without doubt Ger Hungerink's masterpiece.
We must again assume that after White's move, both players will do their best. The incredible idea behind the problem is to self-break a ladder, with a white stone preventing the sacrifice which would end it otherwise (it must be said that this is a Pyrrhic victory for Black, as he destroyed all his territory in the process and loses by three and a half point (Japanese counting) with a 5,5 komi, but this last surprise was difficult to include clearly in the problem caption...). I hope the reader will agree that my rating of     for this tour de force is quite justified... for this tour de force is quite justified...
 Solution 15 : After White's move at 2, the spiral ladder (well-named in this case) ends in a different way... |
|
 ... when the ladder ends (here is an
animated solution), White can no longer play a (even if self captures were allowed, it would be now useless), and Black captures the corner stones, while White lives (and win by 3.5 points)... |
Back to the table of contents
Appendix A: some (badly connected) thoughts upon the "theory" of go problems.
The chess problem theory (or, to be more precise, the exact description of what is a problem, a theme, a key, a demolition, etc.) was much refined in the 20th century, and is now mature ; though I feel chess and go problems have the same potential (and are often of the same quality), go problem theory (in the same accepted sense ot the term) is still in its infancy. I would therefore modestly try here to specify some elements of vocabulary, in order at least to justify the choices made in these pages.
Note first that almost any problem (except perhaps fairy problems, and the emperor of tsumego) can be reduced to the shape "Black to play and win the game" : one has only to surround the problem with a setting giving Black a clear disadvantage if the thematic manoeuvre doesn't succeed ; it is not absolutely true, on the other hand, that every problem can be reduced to a life and death one (some yose problems are clearly not of this type), even if this is very often possible. But here, I will only try to define rules of judgment for problems of "life and death" type, or similar ones, i.e. problems where the objective is clear, and anyone seeing the solution can at least check that it has indeed fulfilled it.
The ultimate question, for our "theory", is what will constitute a good problem. If, in such generality, this is not very clear, one must remember that, in contrast to chess, something very definite exists already in go for individual moves (or in some cases, short sequences) :
the concept of tesuji. Given a competence level (say 3-kyu), "natural" (or ordinay) moves in a given position for this level will constitute a background reference, over which better moves will appear as tesujis. Of course, with this kind of definition, the tesujis of one player will be the bad moves of another...
Nevertheless, it would appear that all strong players agree on what is a tesuji (in the sense of moves above the "ordinary move" level) : the many tesuji dictionnaries compiled by various pros all record the same basic moves, and a complete list of fundamental tesujis (similar to the one I made for the French Go Review) would not differ much from one master to another...
For good foundations of a "go problem theory", it seems therefore necessary to establish a more refined classification. I would not think my star ranking too bad a scale for this purpose, speaking of tesujis for "remarkable" moves in the eye of amateur players (perhaps with a distinction between "basic tesujis" of kyu players, and "advanced tesujis" of dan players), of "exquisite" moves (Japanese myoshu, Chinese miao shou) for moves not obvious to pros, and of "divine" moves (Chinese rushen, entering the divine, feels as poetic as Japanese kami no itte, hand / move of god ; all this terminology will without doubt please Hikaru's fans) for moves one feels are hard to find by mere mortals, as must have been, in a real game, the ear-reddening move, or, in a problem, move 3 of tsumego's empress (well, in the last case, it is not so much finding the move as creating a problem where it appears which feels divinely inspired...)
It then becomes clear that a problem will have value proportionate to the quality and number of its tesujis. But this is certainly not enough. The setting, for instance, would at first sight need to be as light as possible, every stone playing a necessary function. This is obviously something which many problem makers (but not all of them) pay attention to, and some Hatsuyoron problems are even "setting tasks", where for instance a small white corner group faces a dozen black stones on the fourth line, every one of them being necessary to kill unconditionally (recall also the function of the marked stone in problem II.2.14). On the other hand, if these problems are supposed to be used for training, it is then important that the setting looks as game-like as possible, and gives few clues to the solution (as for instance problem I.2.8, with its many intentional wrong tracks) ; these two objectives are clearly contradictory...
Fujisawa Hideyuki, in his commentary on Dosetsu's problem, lavishly praises "the striking novelty of the shapes, the precise calculation of the capturing races, and the delicate balance of the score", all this "elevating that outstanding problem to the status of a lifetime masterpiece". Of course, "the most difficult problem ever" would have its place in history even without these unique characteristics, but one must admit that, for instance, the qualities of
Nakayama's problem, or even of the astonishing "dangos problem", while certainly not to be despised, are in a somewhat lesser category ; our master would have said (in a derogatory tone) that these were "engineer's problems"...
For another approach, let us now consider what constitutes a correct problem, simplifying the question to life-and-death ones. Of course, a caption like "Black to play and live" is without ambiguity (well, as soon as it is understood that seki is a kind of life, and that living in ko is inferior to unconditional life, and therefore is not a proper solution) ; we can consider such a problem solved as soon as the conditions of the caption are satisfied, demolished if this cannot be done, and not correct (or not proper) if there is more than one solution (with a proviso for transposition of moves, as explained below). But what to do with status problems (which, I believe, should be considered as the only valuable ones for training purposes, as no one in a game is there to tell you the result you can get in a given position  ) ? Most of these will have clear answers, but already the "correct" solution to problem I.2.9 is not obvious, as the yoseko resistance of White is so desperate ; I believe no pro would be sure of what the right answer is to problem I.6.5 (and, as a general rule, it is well-known that different kind of indirect kos cannot be compared in the absolute). As was shown in semeais 5 and 6, it is even possible that the only answer, in some situations, is to give different lines of play, and to specify under what external conditions one line should be preferred over another...
) ? Most of these will have clear answers, but already the "correct" solution to problem I.2.9 is not obvious, as the yoseko resistance of White is so desperate ; I believe no pro would be sure of what the right answer is to problem I.6.5 (and, as a general rule, it is well-known that different kind of indirect kos cannot be compared in the absolute). As was shown in semeais 5 and 6, it is even possible that the only answer, in some situations, is to give different lines of play, and to specify under what external conditions one line should be preferred over another...
John Fairbairn, commenting the problems of Xuan Xuan Qi Jing, explains that these positions (and their solutions) were probably not really intended to be perfectly correct, but rather were conceived as "conversation pieces" between amateurs, who could even (as I tried to do for some of the problems here) add some stones of their own to create new wondrous variations, and were perhaps not necessarily looking for some definitive answers...
There is also a slight problem with what constitutes an "answer". I believe Pierre Aroutcheff was the first to point this out clearly, when discussing the related question of tesuji problems. As he notes, there are two completely different brands of tesujis, the "decisive" ones, where playing them or not changes massively the issue of some fight (like the cutting tesujis discussed in section II.4), and the "stylish" ones, which simply improve a local situation (perhaps only by a few points) without having fundamental tactical or strategic consequences (two-step hanes, eye-stealing tesujis, or the classical "extend once before giving up two stones" are examples which should be clear to every confirmed player). In the second case, it makes sense to show, as an answer, how the complete sequence would be played in an actual game (and perhaps compare it with "ordinary" sequences, to show what was gained). But what constitutes an answer in the first case ? At best, one would show the strongest resistance, and prove it fails, but then, obviously, this is not what would be played in a game (this question was discussed at length by James Davies in the first chapter of "Tesuji"), and anyhow what does "the strongest resistance" mean, exactly ?
The idea that, in a problem, some moves are more essential than others can, in many cases, be made objective. The importance of move 1 in
problem II.4.5 is absolute (this is a real "key move") : played later, it will not work at all. The main reason is that it is a probe (a generalisation of the double threat idea, and one of the few concepts which can be easily transposed to other games, at least those with "superposition" properties) : P forces an answer A, or B (in the simplest case), which has a specific counter (a, respectively b). But if one plays a first, B will be the answer (and b would be countered by A), after which P becomes irrelevant... In all similar cases, P is a "key move", and finding it in problems like I.1.1 or II.3.7 gives the solver a characteristic feeling, which Martin Gardner called the "Ah-ah effect"...
In chess problems, the key move must be the first one, and of course unique. These requirements must be somewhat weakened for go : it happens much more often in our game that one may interpose preliminary moves. For instance, in problem II.4.3, the key may in fact be played after the cutting exchanges. But the problem will become clearly less aesthetically pleasing if one eliminates this possibility by giving a setting where those exchanges have already been played ; moreover, if a similar position occurred in an actual game, these exchanges should often stay unplayed (for instance to keep ko threats, or to prepare the yose, etc.). On the other hand, many problems (like II.1.2) are made harder (and often more beautiful) because the key move appears only after a sequence of easier ones, whose reading is already quite difficult ; actually, older chess problems were often of this type ; they were eliminated by history (of chess), but go aesthetics are somewhat different, and it is not clear that the same objections would apply. Last, the order of moves is often also not as essential as in chess : for instance, in problem II.2.10, the "key" 5 (and is it so clear that this is the key move ?) may in fact be played anywhen earlier (but not later...) ; only a chess problemist would feel that this demolishes the problem...
Retour à la table des matières
Appendix B: a few tries at (almost) rigourous definitions.
The technical terms used in this bestiary, while some of them are of my own invention, are well-known or explicit enough to be easily understood by the confirmed player. Nevertheless, a mathematically inclined reader could ask for something more rigourous. The following definitions use as a starting point the japanese analysis of exceptional positions made by the 1989 rules (motivated in part by the need of not counting any territory in sekis), and on their formalization by Robert Jasiek, Berlekamp, and other experts of CGT applied to go, but they are written in reference to AGA rules, which are clearly better fitted to those positions ; I did not wish to give completely formal definitions (on the model of Taylor-Tromp rules, for instance), but I hope the reader will convince himself that doing this would not present real difficulties, even if practical applications, like computer implementation of those terms, could become quite tricky.
James Davies, in "Life and Death", gave definitions, now in common use, of group status (dead, alive, unsettled, alive in indirect ko, etc.) : for instance, a group is dead if it can be captured against any defense, even if the defending side plays first. I used those terms in the tsumego problems of the bestiary, but for the analysis of the fights (semais) of part IV, a more precise vocabulary is necessary.
First, we say that a group (or more exactly a set of connected chains of stones) is independently alive if it can form two real eyes against any attack, even supposing the external opponent stones immortal, and mortal otherwise ; this implies that a mortal group can be captured by a succession of legal moves played while the player owning the group passes continuously (this last definition is equivalent to the previous one if one does not take in account the possibility of eyes so big that they allow the formation of an eye "in the stomac"). A set of groups (of both colours) is then in semeai if they are all mortal and share liberties (an even more formal definition would require minimality, i.e. inexistence of a smaller semai included in the first).
The following definitions assume perfect play from both players after the initial move under scrutiny. A semeai is a complete seki if any further play by any player would lose points by AGA rules (i.e. his opponent could then capture stones, enter some favorable exchange (furikawari), play some dames, etc.) ; a semeai ends in seki if the outcome of the optimal sequence is a complete seki where none of the initial groups has been capturde. Those definitions cover correctly the usual cases (when no ko appears), and could be use to give a formulation of the Japanese rules alomost equivalent to the official one, assuming perfect play ...
When the position is "complete" for only one player, I say it is a semi-complete seki. For instance, in some semeais, moves by one player lose all his groups, while the other player can still win points by AGA rules : those positions are half-sekis when some group can still be captured (the simplest case being the "both dead, only one capturable" position), and sekis with one-sided dames otherwise (as in the reference position of part V). Other situations have stranger behaviour : adding a move gives a worse result than letting the opponent add one (as for a complete seki), but the position is not in seki, as one of the players is still better off by adding the move ; the best known example of this is the "three points without playing" (torazu san moku) position ; the semeai of figure IV.17a is another instance ; those are, in my terminology, pseudo-sekis.
Last, some semeais would be complete sekis if it were not possible to sacrifice a group and get back a larger one in exchange ; those mock sekis (Japanese players could well nickname them imosekis, imo being the (sweet) potato and imosujis those moves which look like tesuji, but are actually weak) cannot appear in fights between less than four groups, and this possibility has therefore few practical consequences, but make quite hard the complete theory of those positions ; on the other hand, the complete seki of figure IV.2.6 is quite a surprise, consequence of a well-hidden possibility ; as perhaps for problem I.5.3 and for the sekis with three mutual liberties in figures IV.3.10 and 11, the fact that no further move can be played without harm is hard to see, even (and perhaps especially) for professionnals...
Back to the table of contents
Back to Part 1
Back to Part 2
|