|
Introduction
I. Problèmes de vie et mort extraordinaires.
II. Tesujis paradoxaux et manœuvres étranges.
III. Shichos et autres séquences incroyables.
IV. Semeais, sekis et pseudo-sekis.
V. Problèmes liés aux règles.
Annexe A : réflexions (mal connectées) sur une "théorie" du problème de go.
Annexe B : quelques tentatives de définitions (presque) rigoureuses
Vers la première partie
Vers la deuxième partie
III. Shichos et autres séquences incroyables.
Il faut bien admettre que la plupart des séquences de cette section sont extrêmement artificielles. Mais cela ne les rend pas moins jolies (ou du moins amusantes), et, comme le dit Cyrano : "Non, non, c'est bien plus beau lorsque c'est inutile..."
Commençons par rappeler que "si vous ne comprenez pas les shichos, ne jouez pas au go". Bon, ça n'a pas l'air si compliqué à comprendre, quoique de nombreuses questions théoriques liées à ces situations, à commencer par le prix qu'on paye en poussant un shicho qui ne marche pas (7 points par poussée), soient plus subtiles qu'on ne le croit. Mais malgré les avertissements de Kageyama dans le premier chapitre de "Lessons in the Fundamentals", tout le monde au-dessus du niveau de 10ème kyu s'imagine être capable de lire un escalier. Et pourtant...
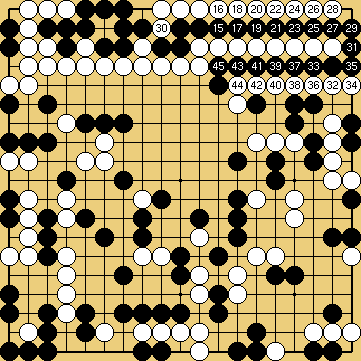
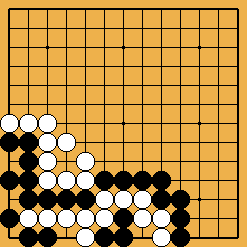
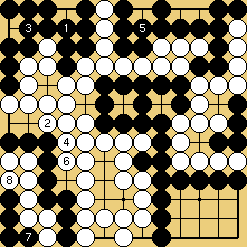
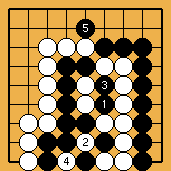
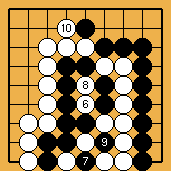
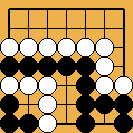
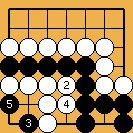
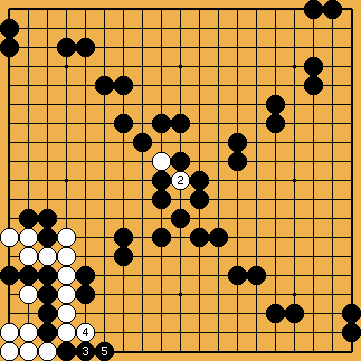
L'invasion du problème 1 est souvent jouée, à haut handicap, par des Blancs qui ne soupçonnent pas à quel point un joueur noir qui "comprendrait" vraiment les shichos pourrait les punir. Le joseki démodé du problème 2 était soigneusement analysé dans le dictionnaire d'Ishida, et y donnait lieu à de forts intéressants développements théoriques (j'ai essayé d'en montrer quelques uns dans ce fichier sgf) ; du temps où on le rencontrait fréquemment en tournoi, les traquenards dont il est truffé (à commencer par celui montré ici) ont souvent procuré aux joueurs français de grandes satisfactions. Enfin (problème 3), la catastrophe survenue à O Meien en 2000 lors de la première partie du 55ème tournoi du Honinbo (voici le fichier sgf de cette partie) montre bien que les joueurs professionnels modernes n'ont plus aucune honte de leurs (rares) moments d'absence : alors que, je le suppose, après une mésaventure pareille, Shusaku, mortifié, se serait retiré quelque temps dans un monastère, O Meien se contenta d'abandonner (en éclatant de rire), puis gagna les parties suivantes, et le titre.
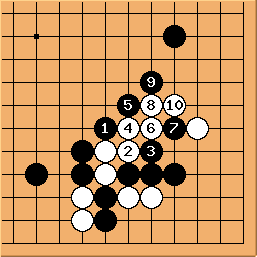
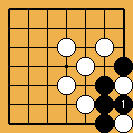
Solution 1 : la pierre blanche ne brise pas le shicho en fait
Solution 1 (suite) : c'est une sorte de squeeze
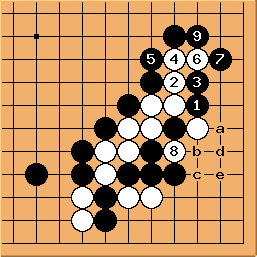
| | 
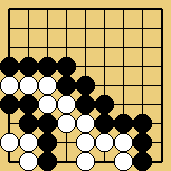
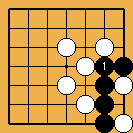
Solution 2 : le shicho part de la première ligne
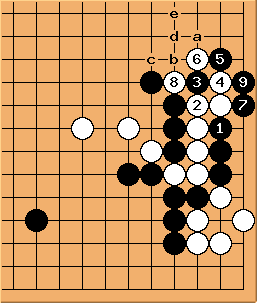
| | 
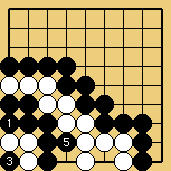
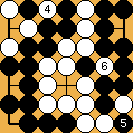
Solution 3 : le mur blanc est avalé au passage (mais O Meien abandonna avant ...)
|
En revanche, il n'y a aucune honte à avoir si vous n'arrivez à résoudre (sans poser de pierres) aucun des problèmes qui suivent...
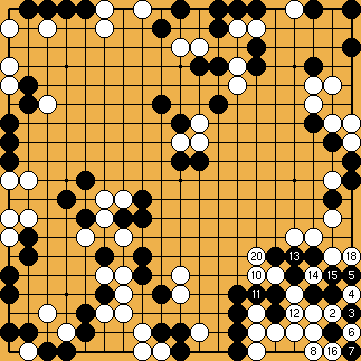
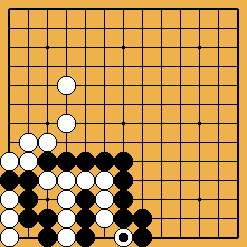
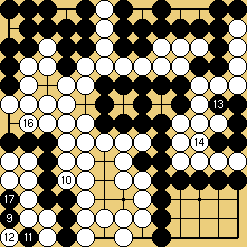
   Problème 4 : Blanc joue et fait vivre le groupe du coin SE Problème 4 : Blanc joue et fait vivre le groupe du coin SE
Certains professionnels se sont spécialisés dans la construction de shichos à ricochets parcourant tout le goban ; le problème 4 est un assez joli exemple, demandant quelques précautions au départ. Ce genre de labyrinthe hautement artificiel, évidemment, peut paraître manquer d'intérêt, mais essayer de les résoudre de tête est à tout le moins un formidable exercice de musculation...
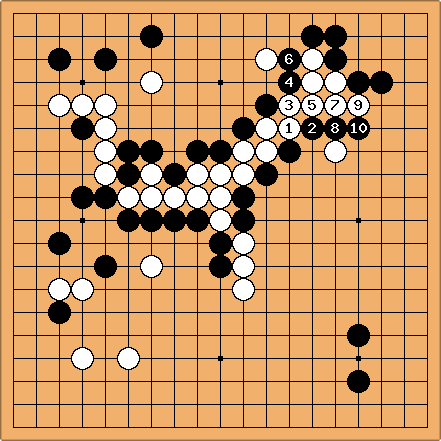
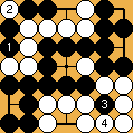
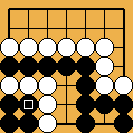
Solution 4 : je ne montre que le départ de l'escalier ;
cliquer ici pour un diagramme animé le montrant en entier
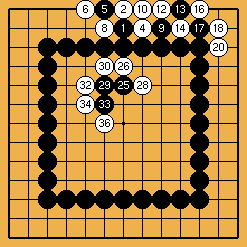
Il existe bien d'autres séquences spectaculaires de ce genre ; Nakayama s'est ainsi spécialisé dans la création de problèmes figuratifs, dont l'énoncé représente des cœurs, des kanjis ou le numéro de l'année... Mais j'ai pu découvrir aussi des "problèmes d'ingénieur", qui ne sont "que" des améliorations, consistant à rajouter un escalier complexe à un autre problème ; le plus étonnant est certainement le suivant :
Ce problème, extrait du Genran (le recueil d'Akubotsu Intetsu dont je parle ici), est une amélioration des idées de sacrifice de Dosaku (voir le problème I.4.12) : l'ishinoshita (qui est donc ici tourné vers le centre) se combine avec un escalier aux innombrables rebondissements.
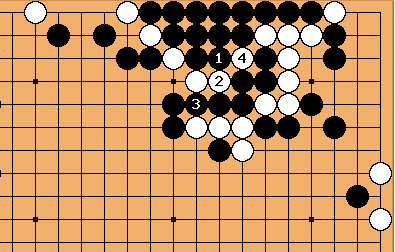
Solution 5 : un sacrifice de 14 pierres
| | 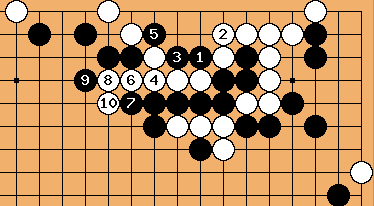
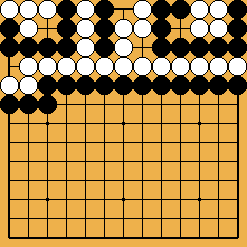
Solution 5 (suite) : les premières marches de l'escalier
| | 
Solution 5 (conclusion) : l'aviez-vous lu jusqu'ici ?
|
À présent, voici des problèmes d'un tout autre genre.
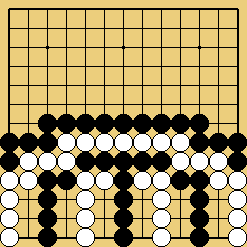
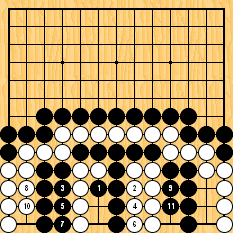
Les problèmes 6 et 7 (améliorations de problèmes chinois classiques que je dois à Pierre Colmez, et qui, contrairement aux autres problèmes de cette section, donneraient presque l'impression d'être tirés de parties réelles) ont pour thème la construction de shichos : dans chaque problème un ou deux groupes peuvent vivre si un certain escalier "marche" ; il faut d'abord trouver lesquels (une opération particulièrement délicate pour le second problème, puisque Pierre et moi avons découvert à l'été 2007 qu'une erreur s'était glissée dans le diagramme de solution, et que personne ne l'avait relevée... depuis près de vingt ans), puis placer un coup qui le fait ou les fait marcher tous les deux.
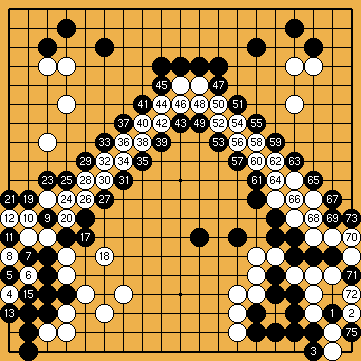
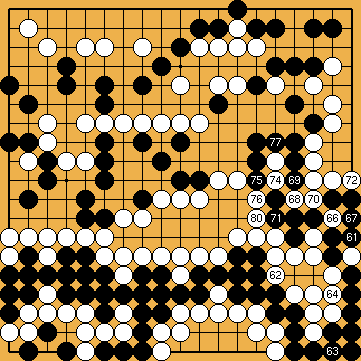
Solution 6 (14 en 11, 16 en 5, 22 en 9, 74 en 71) : le constructeur du shicho est à l'endroit le moins plausible ; ensuite, on admirera le ricochet, et surtout la jolie conclusion en double snappe.
Cliquez pour un diagramme interactif
| |
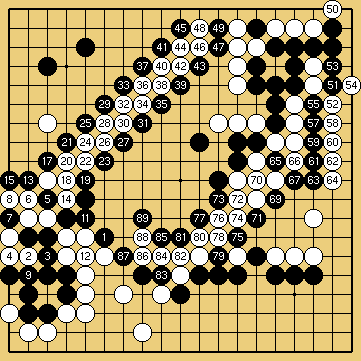
Solution 7 (10 en 7, 16 en 5, 56 au-dessus de 55, 68 en 65) : ici, il faut "construire" les deux shichos ; le second est par ailleurs assez difficile à démarrer...
Cliquez pour un diagramme interactif
|
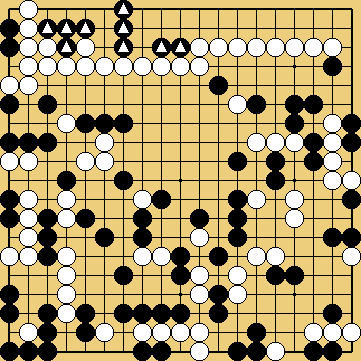
   (?) Problème 8 : Blanc joue et capture les pierres marquées (?) Problème 8 : Blanc joue et capture les pierres marquées
La séquence du problème 8 (que j'ai découvert dans le livre de Nakayama, mais il est dû à Hayashi Genbi, au début du 19ème siècle) est assez étonnante aussi, c'est un chemin de deux libertés (un shicho flou, ou yurumi shicho) parcourant tout le goban.
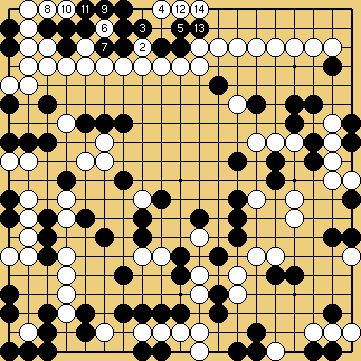
Solution 8a : le début. À présent, Blanc monte
une surprenante attaque par la première ligne...
| 
Solution 8b : ... qui se transforme en chemin de deux libertés | 
Solution 4c : la conclusion : avoir composé ce problème
est un étonnant exploit, et calculer cette séquence sans
poser de pierres est déjà assez dur.
Si vous n'y êtes pas parvenu,
cliquez ici pour une solution interactive. |
    Problème 9 : Blanc joue et sauve les pierres marquées Problème 9 : Blanc joue et sauve les pierres marquées
En un sens, le problème 9 (tiré du Hatsuyoron) est aussi un shicho flou, mais c'est plutôt un exercice de construction de pâtés (dango). Comme très souvent dans ce recueil, il s'agit aussi d'un tour de force (task) : certains des pâtés construits (par exemple le rectangle 3x5 au centre) paraissent détenir le record possible en partant de formes relativement légères. Il est, en outre, presque impossible d'en montrer la solution sous forme de diagrammes, d'où la version interactive proposée plus bas, et l'intérêt des fichiers sgf...
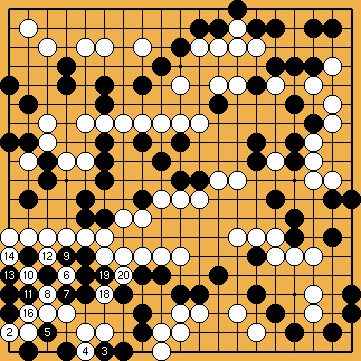
Solution 9a : amorce, et construction d'un grand œil (Blanc a 9 libertés)
| 
Solution 9b : le squeeze se déplace vers le coin
| 
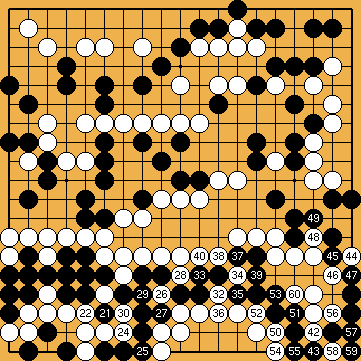
Solution 9c : le premier pâté au centre. Et maintenant ?.
| 
Solution 9d : la conclusion : il faut être assez fort pour pouvoir ressortir ainsi de ce labyrinthe.
Si vous n'y êtes pas parvenu,
cliquez ici pour une solution interactive.
|
Et pour finir, les plus étonnantes constructions de seki que j'aie rencontrées (celle du Hatsuyoron n'est pas à dédaigner, et figurera sûrement tôt ou tard ici, mais me semble légèrement moins complexe ; d'un autre côté, elle est peut-être plus correcte...)
    (?) Problème 10 (No Man's Land) : Blanc joue ; qu'arrive-t-il s'il cherche à sauver le groupe du bord sud? (?) Problème 10 (No Man's Land) : Blanc joue ; qu'arrive-t-il s'il cherche à sauver le groupe du bord sud?
J'ai découvert le problème 10 (No Man's Land) sur ce site très varié de problèmes de tous niveaux. L'énoncé n'est peut-être pas très rigoureux (Blanc joue et gagne la partie serait meilleur...), et il est possible que des erreurs se soient glissées dans cette composition, mais le fait que son auteur soit un joueur en kyu excuse bien des choses, sans parler du fait que les formes sont nettement plus naturelles que dans les compositions classiques sur le même thème...

Solution 10a : seki provisoire. À présent, Noir attaque les groupes extérieurs
| 
Solution 10b : il reste encore un semeai à jouer
| 
Conclusion. Il semble (mais je ne l'ai pas contrôlé) que dans cette version, Blanc gagne d'un demi-point.
Cliquez ici pour voir une solution interactive.
|
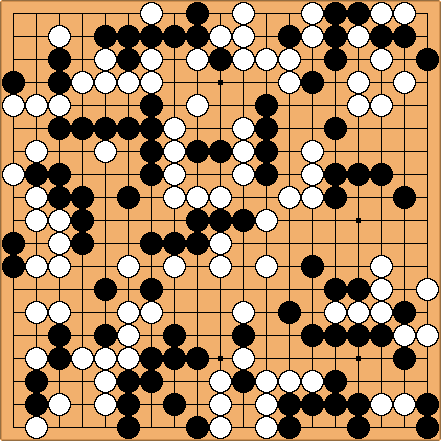
    Problème 11 : Blanc joue ; quel est le résultat ? Problème 11 : Blanc joue ; quel est le résultat ?
(voici un fichier sgf de la solution)
Le problème 11 est l'avant-dernier problème du Genran (le recueil d'Akubotsu Intetsu dont je parle ici), et c'est sans doute le plus beau problème classique de construction de sekis. Là encore, l'énoncé n'est pas très clair (Noir est-il vraiment obligé de défendre le groupe nord-ouest ?), et il est bien possible que des erreurs persistent dans cette composition (en particulier, je ne comprends ni l'ordre des coups au centre, ni le résultat dans le coin sud-est); on trouvera d'autres remarques à ce sujet en annexe... Une solution non commentée (pour l'instant) est donnée dans le fichier sgf associé
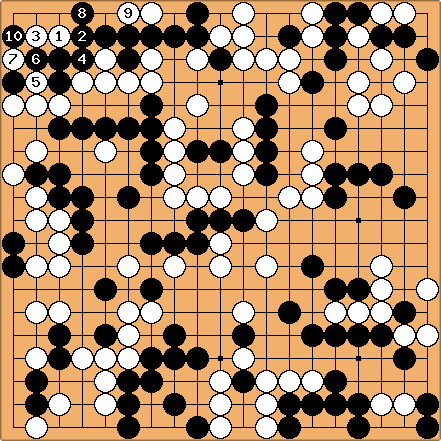
Solution 11a : les 10 premiers coups
| | 
Solution 11b (les derniers coups); si Blanc veut empêcher ce dernier seki, il perd le semeai central !
|
Retour à la table des matières
IV. Semeais, sekis et pseudo-sekis
Les problèmes et les positions de cette section (et de la suivante) sont clairement moins beaux et intéressants que ceux des précédentes. Mais c'est là un de mes sujets favoris (je suis même l'auteur de quelques-unes de ces positions), et je ne pouvais résister à la tentation de présenter ici certains résultats qui surprendraient même les professionnels (mais ne les intéresseraient sans doute guère  ) ... ) ...
Un semeai ("course aux libertés"?), c'est un combat entre deux (ou plusieurs) groupes non vivants, qui ne peut se terminer que par la capture d'un de ces groupes, ou par un équilibre de la terreur (seki). Techniquement, ces définitions manquent de rigueur, et je renvoie à l'annexe B de ce bestiaire pour quelque chose d'un peu plus satisfaisant (les connaisseurs de la règle japonaise savent que définir vraiment rigoureusement un seki relève de l'exploit, même s'il est tout à fait possible d'arriver à quelque chose de raisonnable en pratique)
1. Semeais simples et comptes de libertés
Dans un combat entre deux groupes, celui qui a le plus de libertés gagne... Ce "proverbe pour joueurs faibles" doit déjà être corrigé pour prendre en compte le cas des sekis, et admet bien des exceptions, comme nous allons le voir.
Pour commencer, rappelons le premier cas vraiment intéressant de semeai. À votre avis, qui gagne celui de la figure 1 ?
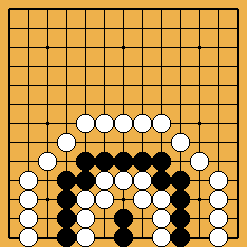
 Figure
1 ("la maisonnette") : « Noir a-t-il vraiment 10 libertés d'avance? » Figure
1 ("la maisonnette") : « Noir a-t-il vraiment 10 libertés d'avance? »
Un proverbe utile ici est "3-5-8-12-17" (bon, pour un proverbe, il manque de qualités littéraires), qui donne le nombre réel de libertés d'un grand œil. Ici, par exemple, Blanc, ayant un œil de 7 espaces où sont déjà posées 2 pierres, a 17-2=15 libertés, ce qui veut dire que celui qui commence la course la gagne d'un temps ; si cela ne vous paraît pas évident, je vous engage à vous en convaincre en posant les pierres sur un goban, ou à l'aide de cette
démonstration interactive.
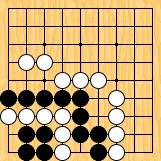
 Figure
2 : dans ce cas, Blanc ne peut pas vraiment compter sur 9 libertés ... Figure
2 : dans ce cas, Blanc ne peut pas vraiment compter sur 9 libertés ...
Ces formules deviendront vraiment utiles dans les analyses de certaines des positions qui vont suivre ; il convient toutefois de préciser qu'elles ne sont pas correctes dans tous les cas, certains "grands yeux" exceptionnels du coin, tel celui de la figure 2, devant perdre beaucoup de leurs libertés pour empêcher qu'il se forme ce que Davies appelle "un œil dans le ventre" ; le lecteur attentif remarquera que c'est l'une des explications de l'étrange seki de la position V.12, et de celui de la figure 3 bis...
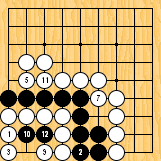
Solution 2 (4 en 10, 6 en 12, 8 à droite de 3) : en fait, Noir gagne d'une liberté.
Une conséquence des formules précédentes est qu'il est normalement impossible d'avoir un seki entre deux groupes ayant des yeux de tailles différentes, parce que le joueur ayant l'œil le plus grand commence par combler toutes les libertés mutuelles sauf une, puis capture les pierres éventuelles intérieures, approche, et gagne la course. Argument bien connu (le proverbe japonais correspondant est "O me, ko me", c'est-à-dire "grand œil / petit œil") et apparemment imparable, qui a été réfuté, à notre grande surprise, par Paul Drouot lors d'un commentaire de partie (alors qu'il n'était que 2ème dan), aboutissant à la position suivante :
Figure
3 : le grand œil de Blanc brise-t-il le seki ?
Je tiens quand même à vous rassurer : l'autre proverbe plus connu ("Me ari, me nashi" = "Un œil contre pas d'œil" = "Au royaume des aveugles, les borgnes sont rois") semble, lui, irréfutable (mais en serez-vous encore si sûrs à la fin de ce bestiaire ? allez donc voir à ce sujet le hanezeki circulaire) La position de la figure 3 me paraîssait un secret français bien gardé, mais j'ai eu la surprise de voir que nos amis britanniques la connaissaient aussi : elle figure dans le livre sur les semeais (Counting Liberties and Winning Capturing Races) publié par la BGA.
Figure
4 : un seki bizarre dû à l'ordinateur
Bien que ce ne soit pas exactement une autre réfutation du proverbe, le semeai de la figure 4, que seul un ordinateur (ou des joueurs très faibles) risquerait de rencontrer, et que j'ai découvert en mars 2008 grâce à un des programmes "MonteCarlo" dont MoGo est le représentant le plus connu, relève du même paradoxe : le joueur ayant le grand œil doit néanmoins le réduire pour amorcer le combat, perdant ainsi son avance en libertés. C'est un seki, et de plus il n'est pas "terminé" : en jouant correctement, Noir peut (à la fin de la partie) encaisser 9 points (en règle française; les japonais n'en compteraient que 6) contre toute défense (évidemment, dès qu'il ne reste plus que 2 libertés mutuelles, Noir doit déclencher les évènements en capturant les trois pierres, et Blanc doit alors surtout... ne pas toucher aux libertés mutuelles)
Solution (2 passe, 4 en 2-2, 6 en 2-1, 7 au-dessus de 3, 8 en 6) : si Noir commence, il encaisse 9 points (les 6 prisonniers, la destruction des deux yeux de l'autre seki, et la pierre jouée en 1)...
En dehors des positions précédentes (et d'une variante plus simple que nous retrouverons au paragraphe sur les règles), la seule autre chose inhabituelle (pour autant qu'on le sache) qui puisse se produire dans des combats sans ko entre deux groupes est le hanezeki (et non hane seki, une erreur que j'ai toujours vu commettre, et qui a été récemment signalé à Harry Fearnley par John Fairbairn) de la figure 5 ci-dessous; cette position étrange, où la pierre marquée ne peut être capturée sans briser le seki, a donné naissance au thème principal du problème de Dosetsu, où ces pierres imprenables malgré les apparences sèment le chaos dans la position blanche. On remarquera qu'elle résulte, elle aussi, de l'écart de libertés entre des yeux de tailles différentes...
 Figure
5 : hanezeki ; la pierre marquée n'est pas capturable. Figure
5 : hanezeki ; la pierre marquée n'est pas capturable.
Bien entendu, en partie réelle, les semeais ne sont pas toujours aussi simples à calculer, les libertés extérieures en particulier étant rarement déjà comblées quand le combat s'engage. De plus, certaines de ces libertés peuvent être rendues inaccessibles, comme c'est le cas dans le joli problème suivant :
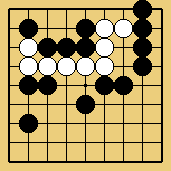
 Problème
6 : Noir joue et gagne le semeai Problème
6 : Noir joue et gagne le semeai
Le groupe du coin ne peut pas vivre (résultat laissé en exercice au lecteur...), mais en menaçant de le faire, et bien qu'il n'ait plus apparemment que 3 libertés, il va gagner le combat...
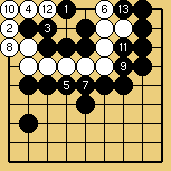
Solution 6 : en fait, Noir gagne d'une liberté, car il se procure trois "temps d'inaccessibilité"
Quand des kos sont en jeu, la théorie des semeais est moins maîtrisée (même si la règle disant qu'il faut jouer le ko en dernier est souvent correcte), mais il faut aller loin pour trouver des situations sinon paradoxales, du moins vraiment étranges ; j'ai découvert au printemps 2007 que les combats mettant en jeu un "quatre courbés dans le coin" peuvent parfois dépendre de la structure exacte des menaces extérieures. Ainsi, dans les deux exemples de combats ci-dessous (apparemment identiques), Noir peut gagner la partie, mais il ne doit pas jouer le semeai de la même manière dans les deux cas ...
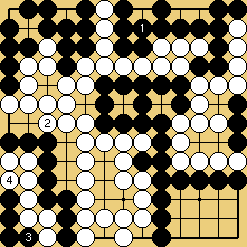
Solution 7 : Noir peut supprimer
une menace de ko blanche, puis...
|
| |
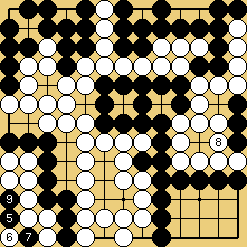
... obliger Blanc à jouer un
ko défavorable
|
Solution 8 : Dans ce cas, Noir peut
supprimer 3 menaces de ko... |
| |
et a encore le temps de jouer
le ko favorable à Blanc, grâce à
sa menace indestructible (15 en 11)
|
2. Semeais entre trois groupes
La situation se complique déjà nettement dans des combats entre trois groupes. Le seki de la figure 1 est bien connu (si ce n'est que beaucoup de "vieux" joueurs sont surpris d'apprendre qu'il rapporte deux points à Blanc en règle française), mais ses analogues (avec des yeux plus grands) ont des comportements bizarres : d'abord, la figure 2 ("deux morts, un seul prenable") est ce que j'appelle un demi-seki : Blanc ne peut plus rien faire; Noir peut, quand il veut (donc après le comblage des dames) capturer le groupe qu'il veut, mais cela fait vivre l'autre. S'il reste des libertés mutuelles, la situation est encore plus étrange : dans la figure 3, Blanc ne peut toujours plus rien jouer, mais quand Noir comble une liberté mutuelle, Blanc doit en faire autant pour finir par se ramener au cas de la figure 2 (sinon, il perd ses deux groupes). Ces positions auraient d'ailleurs pu également apparaître dans la section consacrée aux règles, car il est difficile de lutter contre la démonstration de ce que chacun des deux groupes blancs est mort, ce qui, en règle japonaise, risquerait d'amener à des conséquences fâcheuses ...
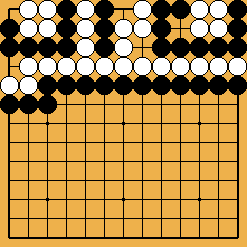
  Figure 4 : un seki complet Figure 4 : un seki complet
   (?) Figure 5 : où est la différence ? (?) Figure 5 : où est la différence ?
|
Figure 4, nous voyons un nouveau type de seki complet (c'est-à-dire une position où rajouter ne serait-ce qu'un coup brise le seki) : les pierres en prise ne sont pas prenables en fait, car le semeai est alors perdu par celui qui les prend. Plus étrange encore, la position de la figure 5 (découverte par André Moussa et moi-même dans les années 85), qui lui semble identique, est en fait un autre genre de demi-seki : Blanc ne peut rien faire, mais quand Noir capture le bloc en carré, puis les 4 autres pierres, Blanc n'a pas le temps de tuer le second groupe et doit se contenter d'un nouveau seki, tandis que Noir a encaissé 11 ou 12 points suivant les règles utilisées (parenthèse : si Noir commence par capturer les 4 pierres en T, c'est alors lui qui perd tous ses groupes ; ce comportement peu intuitif est la raison pour laquelle j'ai donné trois  à cette position). Enfin, il n'y a pas de seki possible entre 3 groupes ayant des yeux plus grands : cette fois, le joueur ayant le plus grand œil a assez de libertés d'avance pour gagner la course... sauf dans un cas parfaitement farfelu, découvert par Harry Fearnley au cours de l'été 2005, et reproduit ci-dessous (figure 7) : dans ce cas (comme dans celui de la figure 1.2), les grands yeux de Blanc sont plus petits qu'ils n'en ont l'air... à cette position). Enfin, il n'y a pas de seki possible entre 3 groupes ayant des yeux plus grands : cette fois, le joueur ayant le plus grand œil a assez de libertés d'avance pour gagner la course... sauf dans un cas parfaitement farfelu, découvert par Harry Fearnley au cours de l'été 2005, et reproduit ci-dessous (figure 7) : dans ce cas (comme dans celui de la figure 1.2), les grands yeux de Blanc sont plus petits qu'ils n'en ont l'air...
Je pensais avoir fait le tour des possibilités de ces combats quand j'ai découvert, durant l'été 2010, la figure 6, qui est encore un seki complet, mais pour une raison fort surprenante : si Noir joue, il perd tous ses groupes, et si Blanc joue, Noir ramène la position à la figure 5, puis encaisse 11 ou 12 points...
|
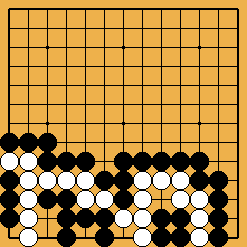
 Figure 8 : un seki dissymétrique Figure 8 : un seki dissymétrique
|
J'ai découvert en août 2004 l'étrange seki complet de la figure 8, réfutant une de mes conjectures (je pensait que les deux groupes blancs devaient avoir des yeux de même taille). Reste-t-il encore d'autres bizarreries de ce genre à découvrir ? Quelque chose d'encore plus étrange que le hanezeki se cache-t-il quelque part ? |
3. Quatre groupes et plus


  Figure 1 : 3 sekis complets Figure 1 : 3 sekis complets
| Au-delà, les combats de 4 groupes et plus ayant peu de chance de se produire en partie, les exemples qui suivent (et dont certains ont été obtenus par la théorie mathématique développée par V. Gurvich) ne seraient donc qu'académiques s'ils ne faisaient pas apparaître de nouveaux phénomènes peu intuitifs : d'abord, les trois roues de la figure 1 sont des sekis complets ; ça peut paraître absurde, puisqu'on passe de l'une à l'autre en comblant les libertés; mais je vous laisse vérifier qu'au lieu d'aller vers le seki suivant, le joueur en second a à chaque fois moyen de gagner le semeai (remarque complètement hors-sujet : j'ai découvert aussi qu'elles donnent naissance à une étrange illusion d'optique : en dépit de ce que vos yeux vous montrent, je peux vous assurer que ces trois diagrammes sont parfaitement carrés...).

|
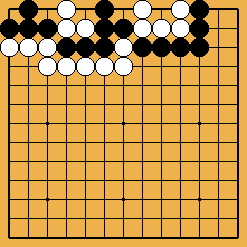
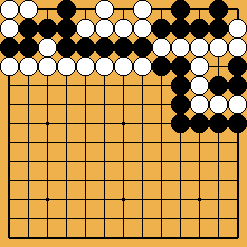
  Figure 2 : sekis et faux sekis (des sacrifices sont possibles dans deux de ces positions) Figure 2 : sekis et faux sekis (des sacrifices sont possibles dans deux de ces positions)
|
Les trois positions enchevêtrées de la figure 2 sont apparemment des sekis complets; mais ce n'est clairement vrai en fait que de la première, car une nouvelle possibilité apparaît : l'un des joueurs peut sacrifier un de ses groupes pour en capturer un autre ! Voilà pourquoi la troisième position est gagnable par Noir (en sacrifiant le groupe du coin), et la seconde n'est un seki complet que parce que si l'un des joueurs essaie de le briser, il y perd deux points...
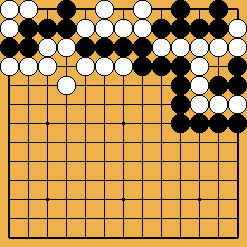
|
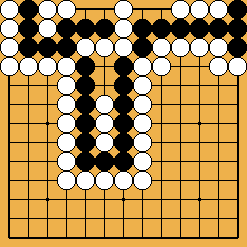
  Figure 4 : encore un exemple de demi-seki Figure 4 : encore un exemple de demi-seki | |
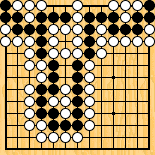
  Figure 5 : un semeai compliqué Figure 5 : un semeai compliqué |
|
Mais la figure 4, elle (que j'ai découverte également en 2004), n'est pas un seki : comme dans la figure 2.2, Noir ne peut plus rien faire pour sauver ses trois groupes; en revanche Blanc peut capturer le groupe qu'il veut, Noir sauver alors celui des deux restants qu'il préfère, et Blanc n'a même plus besoin de capturer le troisième, déjà mort... En 2010, je me suis aperçu que la figure 5 (qui en est l'analogue avec des yeux plus grands) possèdait un statut encore plus complexe : si Noir commence, il parvient seulement à sauver son groupe le plus petit, tandis que si Blanc commence, il capture encore deux groupes, mais Noir sauve le groupe de taille intermédiaire : c'est ce que j'ai appelé un pseudo-seki |
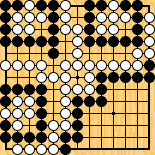
  Figure 6 : un faux seki, trop beau pour être vrai ... Figure 6 : un faux seki, trop beau pour être vrai ... | |
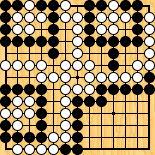
  Figure 7 : un autre semeai difficile Figure 7 : un autre semeai difficile
(voici un fichier sgf de la solution) | |
Revenant, à l'été 2010, sur les calculs qui avaient abouti à la construction de la figure 3, j'ai cru découvrir avec stupeur de nombreux sekis complets à grand nombre de libertés mutuelles, celui de la figure 6 étant sans doute le plus spectaculaire. Il n'est pas très difficile de comprendre ma méprise : si Blanc engage le combat contre un des trois groupes, il doit combler les libertés mutuelles, ce qui revient à dire que le groupe noir attaqué a 11+7=18 libertés effectives, alors que Blanc n'en a que 1+2x(7+1)=17, il perd donc le combat. Mais si c'est Noir qui attaque, tout se passe comme si Noir avait comblé une de ses propres libertés, Blanc contre-attaque alors le groupe qui vient de jouer, et gagne le combat (puisque les deux groupes ont alors le même nombre de libertés). Le lecteur aura déjà compris qu'il se cache une grave erreur de raisonnement dans ce qui précède ; laquelle, et pourquoi la figure 3 ne souffre-t-elle pas du même défaut ? Cependant il reste possible de construire, en suivant le même schéma, des semeais au curieux comportement : dans la figure 7, si Noir commence, il capture le groupe blanc, mais si Blanc commence, il obtient le même genre de résultat que dans la figure 4, capturant deux des groupes noirs, mais le laissant sauver le groupe de taille intermédiaire.
|
Pour finir, voici des exemples à cinq et six groupes : la figure 8 est analogue aux précédentes (Blanc ne peut plus rien faire, et Noir peut capturer le groupe central et celui des deux autres qu'il veut, mais pas les trois) ; Noir doit commencer en a pour capturer le plus grand groupe, ce qui est déjà nettement moins évident... La figure 9 est un semeai dans lequel chacun, pour gagner quelque chose, doit sacrifier un groupe (je laisse le lecteur perfectionniste déterminer lequel, comment et pourquoi) ; dans tous les exemples de ce genre, la séquence optimale est assez difficile à trouver, et on peut aisément perdre tous ses groupes si on s'y prend mal ...
Les figures 10 et 11 (mais pas la figure 12) sont des sekis complets avec 3 libertés mutuelles entre certains groupes ; on ignorait jusqu'en 2011 s'il était possible de faire mieux, sachant que l'exemple avec 4 libertés mutuelles du problème coréen donné dans la section sur les points aveugles "ne compte pas". L'exemple 10 (ou plus exactement une version plus lourde, que j'ai allégée en 1986) a été découvert par V.Gurvich en 1981 (l'objectif principal de cette construction était de mettre en défaut les règles Ing, qui, à l'époque, attribuaient des fractions de points dans les sekis, et prétendaient donner la liste de tous les cas possibles) ; en 2007, j'ai obtenu l'amélioration supplémentaire de la figure 11, éliminant les variantes de sacrifices. Quand à l'exemple 12 (que j'ai également construit en 2007 à l'aide de ses résultats), je le trouve assez élégant, mais hélas, ce n'est pas un seki complet (même s'il faut presque un ordinateur pour s'en convaincre) : il existe (pour les deux joueurs) des variantes de sacrifice (d'ailleurs obligatoires, sinon celui qui remplit une liberté perd tous ses groupes) après lesquelles le score (même en règle chinoise) reste inchangé. Le lecteur parvenu jusqu'ici a sûrement assez de connaissances mathématiques pour comprendre qu'il n'est pas possible d'éliminer ces variantes de sacrifices par le simple expédient consistant à mettre tous les groupes en contact, car le graphe K3,3 ne peut se plonger dans le plan ; voilà pourquoi je suis assez fier de la figure 11...
MISE À JOUR ! (été 2012) En 2011, rééxaminant certaines variations du problème de Dosetsu, Harry Fearnley a découvert un nouveau type de seki, le hanezeki circulaire (figure 13), mettant également au moins 6 groupes en présence (sans parler d'un combat "œil contre pas d'œil" se terminant pourtant en seki), et répondant enfin à la question de Gurvich. Dans l'exemple que je donne, le seki est complet en dépit des 5 libertés mutuelles (si blanc n'avait que 4 libertés, noir capturerait les trois pierres, détruisant le hanezeki, mais gagnant la course ; si noir n'en avait que 4, blanc capturerait la chaîne, se laissant capturer le groupe de coin, mais gagnant la course contre le groupe à un œil) ; le lecteur se convaincra qu'il est possible d'augmenter encore largement ce nombre de libertés mutuelles (mais il ne semble toutefois pas possible de dépasser 14) en variant la taille des différents nakades.
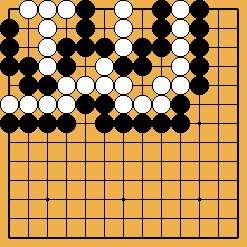
   Figure 10 : un seki complet (mais il y a une variante de sacrifice qui le gâche un peu) Figure 10 : un seki complet (mais il y a une variante de sacrifice qui le gâche un peu) | |
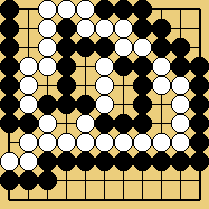
  Figure 11 : verrez-vous pourquoi le sacrifice est impossible ? Figure 11 : verrez-vous pourquoi le sacrifice est impossible ? | |
   (?) Figure 12 : celui-là demanderait presque un ordinateur... (?) Figure 12 : celui-là demanderait presque un ordinateur... |
Explication: après ce sacrifice, par exemple, le score n'a pas changé (vérifiez-le, en n'oubliant pas les nouveaux dames) ... | |
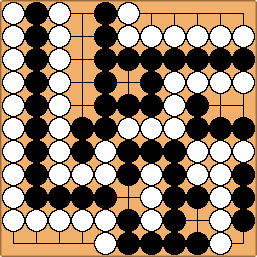
   (?) Figure 13 : Le hanezeki circulaire : les 5 libertés ne peuvent être jouées sans dégâts (?) Figure 13 : Le hanezeki circulaire : les 5 libertés ne peuvent être jouées sans dégâts |
|
Retour à la table des matières
V. Problèmes liés aux règles .
Cette dernière section examine quelques positions ayant posé problème aux joueurs et aux arbitres depuis que le jeu a été pris assez au sérieux pour qu'on tente de le codifier. La plupart sont étudiées, d'un point de vue différent, sur ma page de réflexions sur les règles ; on trouvera ici (parmi d'autres surprises) des positions difficiles à juger en règle japonaise (figures 1, 2, 3 et 4), et des positions amenant à un résultat inattendu en règle française (figures 5 et 10), sans parler du (tristement) fameux ko gluant...
|
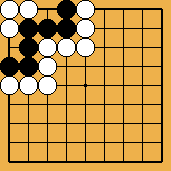
 Figure 1 (référence) : Figure 1 (référence) :
"4 courbés dans le coin"
|
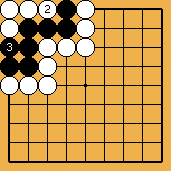
La séquence de capture
(les "4 courbés" sont les 4 pierres blanches sacrifiées) ... |
|
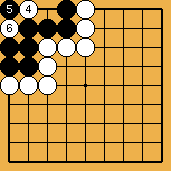
La séquence de capture (suite) :
Noir n'a pas de menace de ko, car la partie est finie |
|
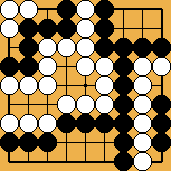
 Figure 2 : le
même, avec une menace de ko indestructible Figure 2 : le
même, avec une menace de ko indestructible
|
La plus connue (et la plus fréquente en partie) de ces positions problématiques est "4 courbés dans le coin" (ou plutôt magari shimoku), le nom traditionnel donné à la position de référence de la figure 1.
Le raisonnement standard rappelé dans les figures suivantes (et qui montre que cette position est encore un demi-seki) s'effondre si Noir possède, comme dans la figure 2, des menaces de ko indestructibles. La règle japonaise (dans sa nouvelle version de 1989) maintient que Noir est mort, et précise suffisament l'analyse pour permettre d'en déduire que Noir est également mort dans la position de la figure 3 (ce qui dépendrait d'éventuelles menaces indestructibles en règle française). J'ai détaillé plus précisément sur ma page de réflexions sur les règles les différentes options qui s'offrent à Blanc dans la position de la figure 2 en règle française ; le lecteur studieux vérifiera que la victoire de 7 points du Blanc en règle japonaise se transforme en défaite de 8 points en règle française s'il trouve la meilleure ligne de jeu (ce qui n'est pas tout à fait évident)...
|
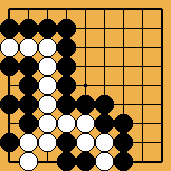
 Figure 3 : 4 courbés dans le coin "généralisé" Figure 3 : 4 courbés dans le coin "généralisé" |
|
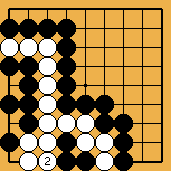
La séquence de capture... |
|
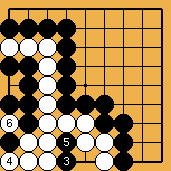
La séquence de capture (suite) : Noir n'a pas de menace de ko, car la partie est finie |
Les raisons justifiant cet étrange traitement par la règle (japonaise) de ces positions exceptionnelles sont essentiellement le désir de pouvoir compter ces situations de pseudo-sekis sans être obligé de les jouer ; c'est ce qui explique aussi la règle jugeant la figure 4 ("torazu sanmoku = trois points sans jouer"), un pseudo-seki dont je donne ici une analyse détaillée en règle française.
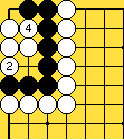
 Figure de référence : 2 et 4 sont des dames unilatéraux Figure de référence : 2 et 4 sont des dames unilatéraux | |
La règle française (s'inspirant de la règle chinoise que, soit dit en passant, on a relativement récemment découvert être en fait postérieure à la version japonaise) évite toutes ces arguties, puisque qu'elle n'utilise pour le décompte final que les pierres effectivement jouées. On trouvera par exemple sur ma page sur la règle française une démonstration de ce que cela ne change le plus souvent pas le vainqueur (ni même vraiment le score), mais il y a évidemment des exceptions (outre l'apparition de points dans les sekis), liées à l'existence, dans certaines positions, de dames jouables par un seul joueur. Son adversaire doit donc passer
pendant ce temps (et payer évidemment la pénalité habituelle si l’on compte
« à la japonaise »). On connaît plusieurs situations de ce type (qui sont, au demeurant,
parfois difficile à jouer de manière optimale quand on n’y a pas réfléchi à
l’avance) : cela peut par exemple se produire pour un ko « d’un
demi-point » en fin de partie, quand on a beaucoup plus de
menaces que l’adversaire : on peut alors le laisser ouvert, puis le
combler, pendant que l’autre ne peut plus que passer (ou jouer dans son
terrain, ce qui revient au même). Des « dames unilatéraux » peuvent aussi apparaître dans certains
sekis par forme. Ainsi, dans le cas de la figure de référence ci-contre, Blanc peut jouer en fin de partie les coups 2 et 4 sans détruire le seki, alors que Noir ne peut plus jouer du tout, car s'il joue en 2, par exemple, Blanc répond en 4 et le groupe noir est mort (« forme en 5 »). Les règles de type chinois vont donc attribuer deux points supplémentaires à Blanc, et la technique de décompte français (dite « méthode de décompte rapide ») obtient ce résultat en obligeant Noir à payer une ou deux pierres de passe (selon que Noir a pu combler ou non le dernier dame extérieur).
|
 Figure 5 : la "vie au clair de lune" ;
les 4 pierres blanches du coin sont-elles vraiment mortes ? |
|
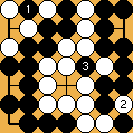 Figure 5 (suite) : en tout cas, on ne peut pas les prendre ! (4 reprend 1) |
Il est clair qu'une règle qui considérerait les 4 pierres blanches du coin NO de la figure 5 comme vivantes serait ressentie par tout joueur non complètement débutant comme un véritable scandale. Et pourtant, on ne peut les capturer : la configuration de droite est ce que j'appelle un seki actif, et Blanc (Noir aussi, d'ailleurs) y dispose d'une infinité de menaces de ko indestructibles, comme on le voit sur la figure suivante. Le scandale évoqué plus haut a donné naissance à deux types de solutions ; comme on pouvait s'y attendre, la règle japonaise a tranché en faveur de la solution "intuitive" , mais par des moyens peu rigoureux (en définissant une notion de vie indépendante assez peu claire) ; il convient de dire qu'en fait, la position a réellement êté adjugée (à Blanc, contrairement à toute vraisemblance) au moyen-âge (c'est le jugement de Nyobutsu), et que l'histoire compliquée de cette règle ne s'est réellement terminée par une victoire de Noir qu'en 1949 ; la règle française permet de réfuter la défense de Blanc en le capturant, s'il persiste, par application de la règle du superko, comme on le voit ci-dessous
 Solution : en règle française, 6 est illégal, car reproduisant la position de la figure 5 ; cette séquence conduit donc Blanc à perdre tous ses groupes. |
|
La règle du superko, ou un équivalent quelconque, par exemple la règle japonaise prévoyant que toute autre répétition qu'un ko annule la partie (mushobu : elle doit être rejouée) est rendue nécessaire par l'existence de quelques situations répétitives classiques autres que des ko : les principaux modèles sont reproduits ci-dessous (la preuve de la nécessité de la séquence est laissée au lecteur  ) ; si le "grand ko" semble quelque peu artificiel, les trois autres cas se sont déjà produits dans des parties professionnelles... ) ; si le "grand ko" semble quelque peu artificiel, les trois autres cas se sont déjà produits dans des parties professionnelles...
   Figure 10 : le groupe du coin NO est-il vraiment vivant en seki ? Figure 10 : le groupe du coin NO est-il vraiment vivant en seki ?
La simplicité de la règle du superko (comparée à la règle japonaise) ne doit pas masquer les considérables difficultés pratiques que créérait, pour les joueurs et les arbitres, son application à des parties de tournoi ; on lui a découvert de plus quelques effets pervers inattendus. Ainsi, la position de la figure 10 présente un seki bien connu ("5 courbés dans le coin")... qui peut être capturé dans ce cas en appliquant à la lettre la règle française, comme on le voit ci-dessous. On pourrait évidemment régler le problème en compliquant légèrement la règle, par exemple (comme l'a récemment proposé Bill Spight) en déclarant que la répétition est légale si l'un des joueurs a passé entre temps (une modification qui résoudrait aussi certains des problèmes posés par le ko gluant), mais outre qu'il n'est jamais sûr que ce genre de modification ad hoc ne crée pas d'autres difficultés inattendues (et demanderait au minimum une formulation garantissant, justement, qu'on ne puisse tranformer un "5 courbés dans le coin" en perpétuel), beaucoup de joueurs ont le sentiment qu'un Noir ayant trouvé la difficile manœuvre de capture mérite bien sa victoire...
 Solution : l'étrange menace de ko 3 (alors qu'il n'y a pas de ko)... |
|
 ... force Blanc à passer au coup 6, puis lui interdit de capturer 5 et 7, puisqu'il reproduirait alors la position de gauche ! |
Le semeai de la figure 11 est sans doute ce qui peut arriver de pire en matière de situation répétitive. Connu sous le nom de "molasses ko" (ou ko gluant), cette position est survenue dans une partie réelle (mais heureusement amicale) de T. Mark Hall, un 4ème dan anglais ; une analyse soignée du combat (faite de manière plus détaillée ici, et sans doute mieux encore dans le fichier sgf correspondant) montre que la séquence de capture donnée dans les diagrammes ci-dessous est continuellement forcée (tant du moins qu'il n'apparait pas de grosses menaces de ko), mais que néanmoins la partie peut continuer à se dérouler à l'extérieur, à 20% de sa vitesse usuelle. Ensuite, une fois les derniers dames comblés, le joueur en retard peut forcer un perpétuel (et donc une annulation de la partie) en règle japonaise, mais hélas, en règle française, on entrerait dans une chose extrêmement étrange et peu intuitive à bien jouer : un "combat de passes", car on voit aisément que le premier joueur à passer se retrouvera empêché de compléter le cycle suivant par la règle du superko (la proposition de Bill Spight mentionnée ci-dessus permet évidemment de régler ce problème, mais, comme on l'a dit, au risque d'en susciter d'autres ...)
 Solution : la séquence est forcée jusqu'au temps de repos 5 ... |
|
 ... auquel Blanc peut enfin répondre au coup 10 |
On pourra trouver d'autres exemples (plus exceptionnels encore, voire franchement inimaginables en partie) de positions créant des difficultés pour certaines règles sur le site de Harry Fearnley, et sur celui de Robert Jasiek.
Pour conclure ce paragraphe, voici à présent l'équivalent goïstique des problèmes d'échecs féériques : quelques possibilités étranges apparaissant lorsqu'on modifie plus radicalement les règles ou les objectifs des problèmes.
  Position 12 : on autorise les suicides ; qu'est-ce que cela change ? Position 12 : on autorise les suicides ; qu'est-ce que cela change ?
La position ci-dessus (due à un compositeur hollandais, Ger Hungerink) est l'exemple le plus simple d'un cas où une autocapture (la règle néozélandaise et celle de Ing les autorisent) provoque un changement de statut (on montre le plus souvent seulement des cas où cela crée de nouvelles menaces de ko, ce qui est nettement moins amusant) : avec les règles usuelles, il s'agit d'un semeai "grand œil contre petit œil", donc perdu par Noir ; mais après que Noir ait capturé ses propres pierres, et bien que ce soit à Blanc de jouer, il ne peut plus faire mieux qu'un seki ...
 Solution : après que Noir ait autocapturé ses quatre pierres ... |
|
 ... Blanc n'a plus qu'un seki |
À présent, trois problèmes à énoncés "différents"...
Dans le premier problème, il faut comprendre (comme dans tout problème d'analyse rétrograde) que le coup cherché doit seulement permettre de satisfaire l'énoncé (et donc qu'il est permis de choisir la position exacte avant le dernier coup du Noir, tant que celle-ci est légale). On en déduit la seule solution possible :
 Solution 13 : le coup que Noir venait de jouer |
|
 Ce que Noir aurait dû faire |
|
Le deuxième problème est une "amélioration" (personnelle, obtenue au congrès de Grenoble en 87) d'une autre création de Ger Hungerink, montrée ci-dessous en variante. Ce type d'énoncé doit normalement être compris en supposant que les deux joueurs jouent optimalement une fois le mauvais coup initial joué (il ne s'agit donc pas de l'analogue d'un mat aidé), mais ici, la situation est bien plus curieuse, un peu comme si on partait d'un groupe noir ayant deux yeux (donc vivant), et que Noir en bouchait un, laissant son groupe mort même si Blanc passait.
Quand au problème 15, les séquences ci-dessous devraient vous convaincre que Noir n'arrive même pas à jouer (sans se faire prendre) ailleurs que sur la seconde et la quatrième ligne ; il meurt donc sans que Blanc ait à fournir de grands efforts ...
 Solution 15 : les pierres noires disparaissent peu après avoir été posées... |
|
Et, pour conclure sur une dernière merveille, voici le chef-d'œuvre incontesté de Ger Hungerink ; l'énoncé devrait vous convaincre de son caractère exceptionnel, mais je ne pense pas que vous parviendrez (des yeux) à le résoudre...
Il faut, là encore, considérer qu'après le coup du Blanc, les deux joueurs jouent normalement. L'invraisemblable idée est d'autodétruire un escalier, en plaçant une pierre blanche à un endroit rendant impossible le sacrifice qui, sans cela, le termine. La séquence de sauvetage du Noir, cela dit, lui coûte la partie, grâce à une autre astuce difficile à inclure de manière rigoureuse dans l'énoncé : Noir a ce faisant détruit tout son territoire, et perd de 3 points et demi (en règle japonaise) si le komi est fixé à 5,5 ! Le lecteur admetra sans doute que tout cela justifie mon classement de ce problème en catégorie     ... ...
 Solution 15 : Après le coup blanc 2, l'escalier en spirale (qui porte bien son nom ici) démarrant ainsi aura une conséquence inattendue... |
|
 ... arrivé là (voici une
solution interactive), Blanc ne peut plus jouer en a (même si on autorisait les suicides, cela n'aurait plus d'intérêt), et Noir peut capturer les pierres du coin, tandis que Blanc vit (et gagne de trois points et demi) ... |
Retour à la table des matières
Annexe A : réflexions (mal connectées) sur une "théorie" du problème de go.
La théorie des problèmes d'échecs (ou plus exactement la description rigoureuse de ce qu'est un problème, un thème, une clé, une réfutation, etc.) a été très développée (surtout à partir du début du 20ème siècle), et si la qualité des problèmes de go et d'échecs me semble être comparable, la théorie du problème de go attend encore ses pionniers. Je voudrais donc modestement tenter ici de préciser quelques éléments de vocabulaire, pour qu'au moins il soit plus facile de justifier les choix faits dans cet article.
On peut déjà remarquer que presque tout problème (sauf peut-être les "féériques", et l'empereur du tsumego) peut se ramener à un problème de la forme "Noir joue et gagne la partie" : il suffit de fermer le reste du goban avec une position donnant un net désavantage à Noir s'il n'arrive pas à exécuter la manœuvre thématique ; il n'est pas tout à fait exact que tout problème puisse en revanche se ramener à un problème de vie et mort (certains problèmes de yose ne sont en particulier clairement pas de ce type), même si c'est très souvent possible. Mais je n'envisagerai ici de définir des critères de jugement que pour des problèmes de vie et mort, ou analogues, c'est-à-dire ayant des objectifs clairs, et pour lesquels tout le monde peut au moins vérifier qu'une solution proposée les satisfait.
Une question fondatrice pour notre "théorie" est de savoir ce qui constitue un bon problème. Si, sous cette forme trop générale, cette question n'appelle pas de réponse claire, on doit se rappeler que, contrairement aux échecs, un critère déjà bien précis semble exister pour les coups individuels (ou parfois les séquences courtes) :
la notion de tesuji. Si l'on se fixe un niveau de compétence (mettons troisième kyu), on peut dire que les coups "naturels" (ou ordinaires) dans une position donnée pour ce niveau vont constituer un fond de référence sur lequel vont se détacher des coups remarquables. On voit qu'avec ce genre de définition, les tesujis des uns sont les mauvais coups des autres ...
Pourtant, il semble bien que tous les joueurs forts s'accordent pour appeler tesuji tout ce qui dépasse le niveau du coup banal : les innombrables dictionnaires de tesuji compilés par les professionnels les plus divers contiennent tous les mêmes coups de base, et une liste complète des tesujis fondamentaux (analogue à celle de mon article dans la RFG) ne connaitrait pas de grands changements d'un maître à un autre.
Dans le cadre d'une "théorie du problème de go", il devient alors nécessaire d'établir une graduation plus précise. En fait, j'aurais tendance à conserver ma notation en étoiles : on parlera de tesujis pour des coups "remarquables" pour des joueurs amateurs (peut-être en séparant les "tesujis de base" des joueurs en kyu, et les "tesujis avancés" des joueurs en dan), de coups "exquis" (myoshu en japonais, miao shou en chinois) pour des coups non évidents pour des professionnels, et de coups "divins" (le terme chinois de rushen, entrant dans la sphère du divin, me paraît aussi poétique que kami no itte, la main (le coup) du dieu, en japonais ; tout cela ravira les fans d'Hikaru) pour des coups qui semblent humainement introuvables, comme l'est, pour une partie réellement jouée, le coup "qui fait rougir les oreilles", ou, pour un problème, le coup 3 de l'impératrice du tsumego (quoique, dans ce dernier cas, ce ne soit pas tant de trouver le coup que de créer le problème où il apparait qui semble relever de l'inspiration divine...)
Il devient alors clair que la valeur d'un problème est plus ou moins proportionnelle à la qualité et au nombre de ses tesujis. Mais ce critère reste insuffisant. Ainsi, la position initiale paraîtrait à première vue devoir être aussi légère que possible, chaque pierre jouant un rôle indispensable. Il est clair que cette question préoccupe de nombreux compositeurs (mais pas tous) : certains problèmes du Hatsutoron sont des "tasks d'énoncé", où par exemple un petit groupe de coin blanc affronte une douzaine de pierres noires sur la quatrième ligne, chacune d'elles étant nécessaire pour tuer inconditionnellement (on pensera aussi à la fonction de la pierre marquée dans le problème II.2.14). D'un autre côté, si ces problèmes doivent être utilisés à des fins d'entraînement, il vaut mieux qu'ils ressemblent le plus possible à des positions tirées de parties réelles, et ne donnent que peu d'indications sur la solution (comme c'est le cas du problème I.2.8, avec ses fausses pistes intentionnelles) : ces deux objectifs sont clairement contradictoires...
Shuko, dans son commentaire du problème de Dosetsu ne tarit pas d'éloges sur "la nouveauté surprenante du thème et des formes, le calcul précis des combats, et l'équilibre délicat des échanges et du score", tout cela "faisant de ce problème exceptionnel, le chef-d'œuvre de toute une vie". Bien sûr, le problème "le plus difficile de tous les temps" aurait même sans cela sa place dans l'histoire, mais il faut reconnaître que, par exemple, les qualités du
problème de Nakayama, ou même de l'étonnant "problème des pâtés", bien que nullement négligeables, sont dans une catégorie un peu inférieure ; notre maître aurait dit (d'un ton légèrement méprisant) que c'étaient "des problèmes d'ingénieur"...
D'un autre point de vue, essayons à présent de voir ce qui constitue un problème correct, en nous limitant aux questions de vie et de mort. Bien sûr, un énoncé tel que "Noir joue et vit" est sans ambiguïté (du moins, dès que l'on sait qu'un seki est une forme de vie, et que vivre en ko étant inférieur à une vie inconditionnelle, cela ne saurait constituer une solution acceptable) ; on peut considérer un tel problème comme résolu dès que les conditions de l'énoncé sont satisfaites, démoli si c'est impossible, et incorrect (ou impropre) s'il y a plusieurs solutions (en étant indulgent pour les interversions de coups, comme cela sera précisé plus loin). Mais les problèmes de "statut" de groupes (qui sont en fait les seuls vraiment pertinents pour l'entraînement des joueurs, puisqu'en partie, il n'y a personne pour vous dire quel est le résultat à atteindre dans telle ou telle position  ) posent d'autres questions : beaucoup d'entre eux ont des réponses claires, mais déjà la "bonne" solution du problème I.2.9 n'a rien d'évident, la résistance de Blanc en ko indirect étant pratiquement désespérée ; je pense qu'aucun pro ne se hasarderait à s"engager sur la meilleure solution du problème I.6.5... Et comme cela fut montré pour les semeais 5 et 6, il peut tout à fait arriver que la seule bonne réponse dans de telles situations soit de donner différentes lignes de jeu, en indiquant dans quelles circonstances extérieures il faut choisir telle ou telle... ) posent d'autres questions : beaucoup d'entre eux ont des réponses claires, mais déjà la "bonne" solution du problème I.2.9 n'a rien d'évident, la résistance de Blanc en ko indirect étant pratiquement désespérée ; je pense qu'aucun pro ne se hasarderait à s"engager sur la meilleure solution du problème I.6.5... Et comme cela fut montré pour les semeais 5 et 6, il peut tout à fait arriver que la seule bonne réponse dans de telles situations soit de donner différentes lignes de jeu, en indiquant dans quelles circonstances extérieures il faut choisir telle ou telle...
John Fairbairn, commentant les problèmes du Xuan Xuan Qi Jing, pense que ces positions (et leurs solutions) n'étaient pas forcément considérées comme parfaitement correctes, mais étaient plutôt conçues comme des occasions, pour des amateurs éclairés, de discuter, de s'émerveiller, et même (comme j'ai tenté de le faire pour certains des problèmes montrés ici) d'ajouter leurs propres pierres pour créer de nouvelles variations extraordinaires sans pour autant être nécessairement à la recherche d'une solution définitive...
Il y a aussi certaines difficultés à définir ce qu'est une "solution". Je pense que Pierre Aroutcheff fut le premier à le dire clairement, dans sa discussion du sujet voisin que sont les problèmes de tesuji. Comme il l'écrit, on peut séparer les tesujis en deux classes, celle des "tesujis décisifs", où le fait de les trouver ou non change de façon massive et immédiate l'issue d'un combat (comme c'est le cas des tesujis de coupe discutés à la section II.4), et celle des "tesujis de principe", qui améliorent simplement une situation locale (parfois seulement de quelques points) sans avoir de conséquences tactiques ou stratégiques essentielles (le double hane, la descente d'une pierre de troisième ligne pour en sacrifier deux, ou les connexions en forme élégante sont des exemples qui viendront aussitôt à l'esprit de tout joueur confirmé). Pour ces derniers, cela a un sens de montrer, comme réponse, la façon dont la séquence complète serait jouée dans une partie réelle (et peut-être de la comparer à la séquence banale, pour voir ce qu'elle rapporte). Mais qu'est-ce qui constitue une réponse au juste, dans le premier cas ? On peut penser qu'il s'agit de la plus forte résistance, et qu'il faut montrer comment elle échoue; mais alors, évidemment, ce n'est pas ce qui serait joué en partie (cette question est longuement discutée par James Davies dans le premier chapitre de "Tesuji"), et de toute façon, que signifie au juste "la plus forte résistance" ?
L'idée selon laquelle certains coups d'une solution sont plus importants que d'autres peut, dans de nombreux cas, être rendue objective. L'importance du coup 1 du
problème II.4.5
est absolue (c'est une vraie "clé") : joué ensuite, il ne marche plus du tout. La raison principale est que c'est un sondage de réaction (une généralisation de la notion de double menace, et un des rares concepts qui se transposent bien à d'autres jeux possédant des propriétés de "superposition") : P force une des deux réponses A ou B (dans le cas le plus simple), qui possèdent une "réfutation" spécifique (a, ou respectivement b). Mais si on joue a d'abord, B sera la réponse (et b serait contré par A), après quoi P devient hors-sujet... Dans tous les cas semblable, P est un "coup clé", et le trouver dans des problèmes tels que I.1.1 ou II.3.7 donne au chercheur une sensation caractéristique, que Martin Gardner a appelée "l'effet ah-ah"...
Dans les problèmes d'échecs, la clé doit être jouée en premier, et bien sûr être unique. Ces
exigences doivent être un peu affaiblies au go : il y est beaucoup plus fréquent qu'on puisse interposer des coups préliminaires. Prenons par exemple le problème II.4.3 : la clé peut en fait être précédée des échanges créant les coupes. Mais le problème sera nettement moins esthétique si on élimine cette possibilité en le posant une fois les échanges joués ; de plus, en terme de jeu pratique, ces échanges devraient souvent restés non joués (pour conserver par exemple des menaces de ko, ou améliorer le yose, etc.). D'autre part, de nombreux problèmes (par exemple II.1.2) sont rendus plus difficiles (et souvent plus beaux) parce que le coup critique n'apparaît qu'après une série de coups plus faciles, mais dont la lecture est déjà délicate ; au passage, signalons que les problèmes d'échecs anciens étaient souvent de ce type ; l'histoire (du problème d'échecs) les a rejetés, mais l'esthétique du go est un peu différente, et il ne semble pas aussi clair qu'il faille critiquer ce modèle. Enfin, les situations où l'ordre des coups n'est pas absolument essentiel sont beaucoup plus nombreuses au go qu'aux échecs : ainsi, dans le problème II.2.10, la "clé" 5 (et d'ailleurs, dans ce cas, quel est le coup qui mérite ce nom, au juste ?) peut en fait être jouée n'importe quand avant (mais tout de même pas après...) ; seul un problémiste échiquéen estimerait que le problème en est gâché...
Retour à la table des matières
Annexe B : quelques tentatives de définitions (presque) rigoureuses.
Les différents termes utilisés dans ce bestiaire (certains étant d'ailleurs de mon invention) sont suffisament connus ou explicites pour ne guère poser de problèmes au joueur confirmé. Cependant, un lecteur d'esprit plus mathématique pourrait souhaiter quelque chose de plus rigoureux. Les définitions qui suivent s'appuient sur l'analyse faite par la règle japonaise de 1989 des positions exceptionnelles (motivée en particulier par le désir de ne pas compter de points dans les sekis), ainsi que sur les études plus rigoureuses encore qui en ont été faites par Robert Jasiek, et aussi par Berlekamp et d'autres experts de la théorie de Conway appliquée au go, mais elles utilisent la règle française, bien mieux adaptée à ces positions ; je n'ai pas souhaité en donner une formulation vraiment parfaite (sur le modèle, par exemple, de la règle néozélandaise), mais on se convaincra, je l'espère, que la chose ne présente pas de difficulté importante (même si d'éventuelles applications pratiques, telles qu'une implémentation informatique, pourrait se révéler fort délicate).
Des définitions classiques du statut d'un groupe (mort, vivant, dépendant de l'initiative ("unsettled"), mort par ko indirect, etc.) ont été données par James Davies dans "Life and Death" : par exemple un groupe est mort s'il est capturable contre toute défense, même en jouant le premier. J'ai utilisé cette terminologie dans les problèmes de vie et mort présentés ici, mais pour l'analyse des combats (semais) de la partie IV, un vocabulaire plus précis est nécessaire.
Tout d'abord, on dira qu'un groupe (ou plus précisément un ensemble de chaînes de pierres) est absolument vivant s'il peut former deux vrais yeux contre toute attaque, même en supposant les pierres extérieures invulnérables, et instable sinon ; cela implique qu'un groupe instable peut être capturé par une suite de coups légaux tandis que le joueur de sa couleur passe continuellement (et cette définition est équivalente à la précédente si on n'envisage pas le cas d'yeux si grand que l'on peut y former un œil "dans l'estomac"). Un ensemble de groupes (des deux couleurs) est alors dit en semeai s'ils sont tous instables et partagent des libertés communes (pour être plus rigoureux encore, il faut aussi qu'on ne puisse pas décomposer cet ensemble en somme de semeais plus petits et indépendants).
Les définitions suivantes supposent que les deux joueurs jouent parfaitement après le coup initial qu'on veut analyser. Un semeai est dit en seki complet si tout coup rajouté par chacun des deux joueurs lui ferait perdre des points en règle française (autrement dit, s'il permettrait à son adversaire de capturer une chaîne, de rajouter des dames, d'entre dans un échange (furikawari) favorable, etc.) ; on dit qu'un semeai se termine en seki si le résultat de la séquence optimale est un seki complet (dans lequel aucun des groupes initiaux n'a été capturé). Ces définitions couvrent assez bien les cas courants (du moins ceux où il n'apparaît pas de ko), et permettent de formuler une variante de la règle japonaise à peu près équivalente à la règle officielle (si l'on suppose que les deux joueurs jouent parfaitement...)
Quand la position n'est "complète" que pour un des deux joueurs, je parle alors de seki semi-complet. Ainsi, dans certains semeais, l'un des joueurs n'a plus de coups ne perdant pas tous ses groupes, tandis que l'autre peut encore améliorer son score en règle française : j'appelle ces positions des demi-sekis lorsqu'une capture de groupe est encore possible (le cas le plus simple étant la position dite "deux morts, un seul prenable"), et des sekis à dames unilatéraux sinon (comme pour la position de référence de la section V). D'autres situations ont un comportement plus étrange : rajouter un coup donne un plus mauvais résultat que de laisser l'adversaire en rajouter un (comme pour un seki complet), mais la position n'est cependant pas un seki, car l'un des joueurs a tout de même intérêt à jouer pour marquer des points ; la position la plus connue de ce type correspond à la règle japonaise dite "trois points sans jouer" (torazu san moku), et c'est aussi le cas du semeai de la figure IV.17a ; j'ai décidé d'appeler ces situations des pseudo-sekis.
Enfin, certains semeais seraient des sekis complets s'il n'était pas possible de sacrifier un groupe pour en capturer un autre plus gros ; ces faux sekis (que Michel Dumont aurait sans doute appelé des sekis hongrois, puisqu' hongrois que le semeai est fini, et qu'on verrait bien les japonais appeler des imosekis) ne se produisent que dans des combats mettant en jeu au moins quatre groupes, et cette possibilité n'a donc que peu de conséquences pratiques, mais rend redoutable l'analyse théorique complète de ces positions ; inversement, le fait que la figure IV.2.6 soit un seki complet est un autre résultat surprenant, et dû lui aussi à une manœuvre bien cachée ; la complètude de ce seki, comme de celui du problème I.5.3 et de ceux à trois libertés mutuelles des figures IV.3.10 et 11, est difficile à voir, même (et peut-être surtout) pour des professionnels. Quand au hanezeki circulaire, sa découverte en 2011, un peu passée inaperçue des experts, montre qu'il reste sans doute encore bien des surprises possibles...
Retour à la table des matières
|